某学校规定，该学校教师的每人每月用电量不超过A度，那么这个月只需交10
元电费，如果超过A度，则这个月除了仍要交10元用电费外，超过部分还要按每度
元交费．⑴胡教师12月份用电90度，超过了规定的A度，则超过的部分应交电费多少元？（用含A的代数式表示）
⑵下面是该教师10月、11月的用电情况和交费情况：
| 月份 |
用电量(度) |
交电费总额(元) |
| 10月份 |
45 |
10 |
| 11月份 |
80 |
25 |
根据上表数据，求A
值，并计算该教师12月份应交电费多少元？
先化简，再求值：6x2-(2x+1)(3x-2)+(x+3)(x-3)，其中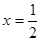
因式分解
（1）﹣2a3+12a2﹣18ª
（2）（x2+4）2-16x2
（3）（x2-2x）2+2(x2-2x)+1
计算
（1）
（2）（-2x）3-(-x)(3x)2（3）
一张矩形纸片，剪下一个正方形，剩下一个矩形，称为第一次操作；在剩下的矩形纸片中再剪下一个正方形，剩下一个矩形，称为第二次操作；；若在第n次操作后，剩下的矩形为正方形，则称原矩形为n阶奇异矩形．如图1，矩形ABCD中，若AB=2，BC=6，则称矩形ABCD为2阶奇异矩形．
（1）判断与操作：如图2，矩形ABCD长为5，宽为2，它是奇异矩形吗？如果是，请写出它是几阶奇异矩形，并在图中画出裁剪线；如果不是，请说明理由．
（2）探究与计算：已知矩形ABCD的一边长为20，另一边长为a（a＜20），且它是3阶奇异矩形，请画出矩形ABCD及裁剪线的示意图，并在图的下方写出a的值．
（3）归纳与拓展：已知矩形ABCD两邻边的长分别为b，c（b＜c），且它是4阶奇异矩形，则b:c=___________________________________________（写出所有值）．
D、E分别是△ABC的边AB、AC的中点．O是平面上的一动点，连接OB、OC，G、F分别是OB、OC的中点，顺次连接点D、E、F、G．
(1)如图1，当点O在△ABC内时，求证：四边形DEFG是平行四边形；
(2)若点O在△ABC外，其余条件不变，点O的位置应满足什么条件，能使四边形DEFG是菱形？请在画2中补全图形，并说明理由．