(本小题满分12分)某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有
次选题答题的机会，选手累计答对
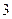题或答错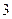题即终止其初赛的比赛：答对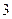题者直接进入决赛，答错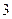题者则被淘汰．已知选手甲答对每个问题的概率相同，并且相互之间没有影响，答题连续两次答错的概率为
．
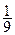⑴求选手甲可进入决赛的概率；
⑵设选手甲在初赛中答题的个数为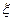
，试求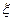的分布列，并求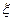的数学期望．
（本小题满分12分）已知数列
满足
，
（
）．
（Ⅰ） 证明数列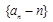
是等比数列，并求出数列的通项公式；
（Ⅱ）设
，数列
的前n项和为
，若对于任意，都满足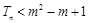
成立，求实数m的取值范围．
（本题12分）数列{xn}满足x1＝1，x2＝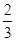
，且
＋
＝
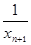(n≥2)，
（Ⅰ）求数列{xn}的通项公式；
（Ⅱ）令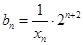
，求数列{bn}的前n项和
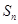的值.
如图所示，在山顶铁塔上B处测得地面上一点A的俯角为α，在塔底C处测得A处的俯角为β.已知铁塔BC部分的高为h，求出山高CD.
（本题12分）已知等比数列{an}的公比q＝3，前3项和S3＝
.
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)若函数f(x)＝Asin(2x＋φ)(A>0,0<φ<π)在x＝
处取得最大值，且最大值为a3，
求函数f(x)的解析式．
已知|a|＝1，a·b＝
，(a－b)·(a＋b)＝，
求：(1)a与b的夹角；
(2)a－b与a＋b的夹角的余弦值．