如图,F是抛物线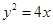 的焦点,Q是准线与x轴的交点,直线
的焦点,Q是准线与x轴的交点,直线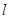 经过点Q。
经过点Q。
(Ⅰ)直线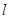 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求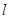 方程;
方程;
(Ⅱ)直线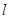 与抛物线交于A、B两点;
与抛物线交于A、B两点;
(i)设FA、FB的斜率分别为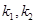 ,求
,求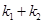 的值;
的值;
(ii)若点R在线段AB上,且满足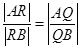 ,求点R的轨迹方程。
,求点R的轨迹方程。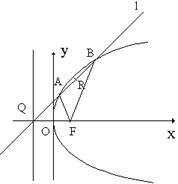
(本小题满分12分)如图,正四棱锥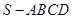 的底面是边长为
的底面是边长为 的正方形,侧棱长是底面边长为
的正方形,侧棱长是底面边长为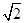 倍,
倍, 为底面对角线的交点,
为底面对角线的交点,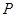 为侧棱
为侧棱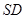 上的点.
上的点.
(1)求证: ;
;
(2)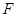 为
为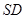 的中点,若
的中点,若 平面
平面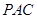 ,求证:
,求证: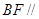 平面
平面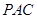 .
.
(本小题满分12分)某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组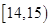 ,…,第五组
,…,第五组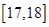 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.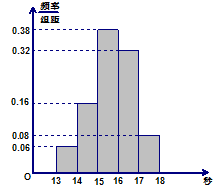
(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数.
(本小题满分10分)已知向量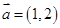 ,向量
,向量 .
.
(1)若向量 与向量
与向量 垂直,求实数
垂直,求实数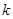 的值;
的值;
(2)当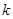 为何值时,向量
为何值时,向量 与向量
与向量 平行?并说明它们是同向还是反向.
平行?并说明它们是同向还是反向.
在锐角三角形 中,
中, 分别是角
分别是角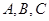 所对的边,且
所对的边,且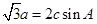 .
.
(1)确定角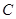 的大小;
的大小;
(2)若 ,且
,且 的面积为
的面积为 ,求
,求 的值.
的值.
某工厂经过技术改造后,降低了能源消耗,经统计该厂某种产品的产量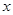 (单位:吨)与相应的生产能耗
(单位:吨)与相应的生产能耗 (单位:吨)有如下几组样本数据:
(单位:吨)有如下几组样本数据:
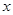 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
根据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率为0.7.已知该产品的年产量为10吨,则该工厂每年大约消耗的汽油为多少吨?