如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y＝
上运动，湖面风平浪静，双帆远影优美，训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．
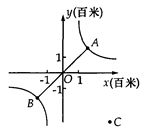
发现C船时，A、B、C三船所在位置的坐标分别为A(_______，_______)、B(_______，_______)和C(_______，_______)；
发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由
如图，AB ∥CD∥GF，∠1：∠Ｄ：∠Ｂ＝2：3：4，求∠1的度数？ 
已知∠AGE=∠DHF，∠1＝∠2，则图中的平行线有几对？分别是？为什么？
如图，AB∥CD，直线FG平分∠AOE，∠1＝40°,则∠2是多少度？ 
如图，已知抛物线
经过
，
两点，顶点为
．
（1）求抛物线的解析式；
（2）将
绕点
顺时针旋转90°后，点
落到点
的位置，将抛物线沿
轴平移后经过点，求平移后所得图象的函数关系式；
（3）设（2）中平移后，所得抛物线与轴的交点为
，顶点为
，若点
在平移后的抛物线上，且满足
的面积是
面积的2倍，求点的坐标．
某企业信息部进行市场调研发现：
信息一：如果单独投资A种产品，所获利润yＡ(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表：
| x(万元) |
1 |
2 |
2.5 |
3 |
5 |
| yＡ(万元) |
0.4 |
0.8 |
1 |
1.2 |
2 |
信息二：如果单独投资B种产品，则所获利润yＢ(万元)与投资金额x(万元)之间存在二次函数关系：yＢ＝ax2+bx，且投资2万元时获利润2.4万元，当投资4万元时，可获
利润3.2万元．
(1)求出yＢ与x的函数关系式．
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yＡ与x之间的关系，并求出yＡ与x的函数关系式．
(3)如果企业同时对A、B两种产品共投资15万元，请设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？