某企业信息部进行市场调研发现:
信息一:如果单独投资A种产品,所获利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
| x(万元) |
1 |
2 |
2.5 |
3 |
5 |
| yA(万元) |
0.4 |
0.8 |
1 |
1.2 |
2 |
信息二:如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获 利润3.2万元.
利润3.2万元.
(1)求出yB与x的函数关系式.
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yA与x之间的关系,并求出yA与x的函数关系式.
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
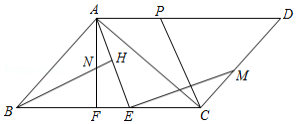
如图,在平面直角坐标系中,抛物线 与 轴交于点 , (点 在点 的左侧),交 轴于点 ,点 为抛物线的顶点,对称轴与 轴交于点 .
(1)连结 ,点 是线段 上一动点(点 不与端点 , 重合),过点 作 ,交抛物线于点 (点 在对称轴的右侧),过点 作 轴,垂足为 ,交 于点 ,点 是线段 上一动点,当 取得最大值时,求 的最小值;
(2)在(1)中,当 取得最大值, 取得最小值时,把点 向上平移 个单位得到点 ,连结 ,把 绕点 顺时针旋转一定的角度 ,得到△ ,其中边 交坐标轴于点 .在旋转过程中,是否存在一点 ,使得 ?若存在,请直接写出所有满足条件的点 的坐标;若不存在,请说明理由.
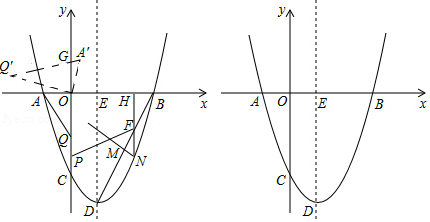
如图,在平行四边形 中,点 在边 上,连接 , ,垂足为 ,交 于点 , ,垂足为 , ,垂足为 ,交 于点 ,点 是 上一点,连接 .
(1)若 , , ,求 的面积.
(2)若 , ,求证: .
某文明小区有50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有 和 参加了此次活动.为提高大家的积极性,6月份准备把活动一升级为活动二:“垃圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加 ,每户物管费将会减少 ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加 ,每户物管费将会减少 .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少 ,求 的值.
在初中阶段的函数学习中,我们经历了“确定函数的表达式 利用函数图象研究其性质一一运用函数解决问题“的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义 .
结合上面经历的学习过程,现在来解决下面的问题在函数 中,当 时, ;当 时, .
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;
(3)已知函 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.

《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征.在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特殊的自然数 “纯数”.
定义;对于自然数 ,在计算 时,各数位都不产生进位,则称这个自然数 为“纯数”,
例如:32是”纯数”,因为计算 时,各数位都不产生进位;
23不是“纯数”,因为计算 时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.