如图(1),在直角梯形OABC中,BC∥OA,∠OCB=90°,OA=6,AB=5,cos∠OAB=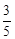 .
.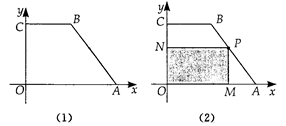
写出顶点A、B、C的坐标;
如图(2),点P为AB边上的动点(P与A、B不重合),PM⊥OA,PN⊥OC,垂足分别为M,N.设PM=x,四边形OMPN的面积为y.
①求出y与x之间的函数关系式,并写出自变量x的取值范围;
②是否存在一点P,使得四边形OMPN的面积恰好等于梯形OABC的面积的一半?如果存在,求出点P的坐标;如果不存在,说明理由.
解方程组: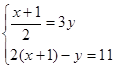
解不等式,并将解集表示在数轴上。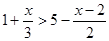
解方程: 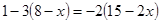
仁寿县交警大队一辆警车沿着一条南北方向的公路巡视,某天早晨从A地出发,晚上到达B地,约定向北为正方向,当天行驶记录如下(单位:千米)+18.3,-9.5,+7.1,-14,-6.2,+13, -6.8,-8.5。问:
(1)B地在 A地哪个方向?相距多少千米?
(2)若该警车每小时蚝油3.35升,那么该天共耗油多少升?(结果保留两个有效数字)
(3)若油箱中有250升油,中途是否需要加油?若需要,至少加多少升?
某市有甲、乙两种出租车,他们的服务质量相同.甲的计价方式为:当行驶路程不超过3千米时收费10元,每超过1千米则另外收费1.2元(不足1千米按1千米收费);乙的计价方式为:当行驶路程不超过3千米时收费8元,每超过1千米则另外收费1.8元(不足1千米按1千米收费).某人到该市出差,需要乘坐的路程为x千米.
(1)用代数式表示此人分别乘坐甲、乙出租车各所需要的费用;
(2)假设此人乘坐的路程为13千米多一点,请问他乘坐哪种车较合算?