已知13 =" 1" =
×12×22, 13+23=9=×22×32,13 + 23 + 33 =" 36" =×32×42, …，按照这个规律完成下列问题：
(1)13+23+33+43+53=________=× ( )2 × ( )2
(2)猜想：13+23+33+…+n3=___________
(3)利用(2)中的结论计算：（写出计算过程）
113+123 + 313+143 + 153+163 + ……+393+403.
如图所示，在△ABC中，∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB，垂足为E，若AB=10cm，求△DBE的周长．
如图，OC是∠AOB的角平分线，P是OC上一点，PE⊥OA交OA于E，PF⊥OB 交OB于F，Q是OC上的另一点，连接QE，QF．求证：QE=QF．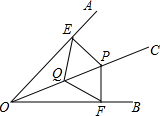
如图，已知CD⊥AB于D，BE⊥AC于E，CD交BE于点O．
①若OC=OB，求证：点O在∠BAC的平分线上．（提示：连接AO）
②若点O在∠BAC的平分线上，求证：OC=OB．
如图，在△ABC中，AD平分∠BAC，AB=6，AC=4，△ABD的面积等于9．
求：△ADC的面积．
如图，已知∠ADC=∠ABC，DE、BF分别平分∠ADC和∠ABC，且∠1=∠2，试说明AB∥DC的理由．