如图所示，在△ABC中，∠C90°，ACBC，AD是∠BAC-优题课

为了响应市政府创建文明城市的号召，某校调查学生对市“文明公约十二条”的内容了解情况，随机抽取部分学生进行问卷调查，问卷共设置“非常了解”、“比较了解”、“一般了解”、“不了解”四个选项，分别记为 $A$ 、 $B$ 、 $C$ 、 $D$ ，根据调查结果绘制了如图尚不完整的统计图．

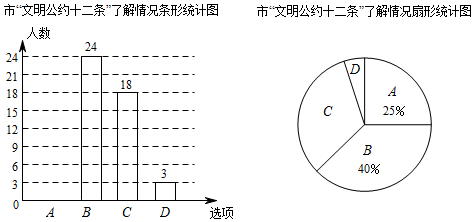
请解答下列问题：

（1）本次问卷共随机调查了　　学生，扇形统计图中 $C$ 选项对应的圆心角为　　度；

（2）请补全条形统计图；

（3）若该校有1200名学生，试估计该校选择“不了解”的学生有多少人？

如图，在 $▱ ABCD$ 中，点 $E$ 、 $F$ 分别在 $BC$ 、 $AD$ 上， $AC$ 与 $EF$ 相交于点 $O$ ，且 $AO = CO$ ．

（1）求证： $ΔAOF ≅ ΔCOE$ ；

（2）连接 $AE$ 、 $CF$ ，则四边形 $AECF$ 　　（填“是”或“不是” $)$ 平行四边形．

某停车场的收费标准如下：中型汽车的停车费为15元 $/$ 辆，小型汽车的停车费为8元 $/$ 辆．现在停车场内停有30辆中、小型汽车，这些车共缴纳停车费324元，求中、小型汽车各有多少辆？

解不等式 $2 x - 1 > \frac{3 x - 1}{2}$ ．

解：去分母，得 $2 (2 x - 1) > 3 x - 1$ ．

$\dots$

（1）请完成上述解不等式的余下步骤：

（2）解题回顾：本题“去分母”这一步的变形依据是　　（填“ $A$ ”或“ $B$ ” $)$ ．

$A$ ．不等式两边都乘（或除以）同一个正数，不等号的方向不变；

$B$ ．不等式两边都乘（或除以）同一个负数，不等号的方向改变．

计算：

（1） $| - 3 | + {(π - 1)}^{0} - \sqrt{4}$ ；

（2） $\frac{x + 1}{2 x} \div (1 + \frac{1}{x})$ ．