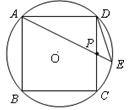
如图，已知：边长为1的正方形ABCD内接于⊙O，P为边CD的中点，直线AP交圆于E点．求弦DE的长；
若Q是线段BC上一动点，当CQ长为何值时，三角形ADP与以Q，C，P为顶点的三角形相似。
已知点A（6，0）及在第一象限的动点P（x，y），且2x+y=8，设△OAP的面积为S．
（1）试用x表示y，并写出x的取值范围；
（2）求S关于x的函数解析式；
（3）△OAP的面积是否能够达到30？为什么？
如图，在
ABCD中，BE交对角线AC于点E，DF∥BE交AC于点F．
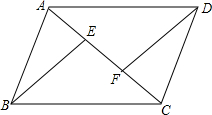
（1）写出图中所有的全等三角形（不得添加辅助线）；
（2）求证：BE=DF．
有甲、乙两种车辆参加来宾市“桂中水城”建设工程挖渠运土，已知5辆甲种车和4辆乙种车一次可运土共140立方米，3辆甲种车和2辆乙种车一次可运土共76立方米．求甲、乙两种车每辆一次可分别运土多少立方米？
某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查，并将调查结果绘制成如图图表：
| 项目 |
篮球 |
乒乓球 |
羽毛球 |
跳绳 |
其他 |
| 人数 |
a |
12 |
10 |
5 |
8 |
请根据图表中的信息完成下列各题：
（1）本次共调查学生名；
（2）a=，表格中五个数据的中位数是；
（3）在扇形图中，“跳绳”对应的扇形圆心角是°；
（4）如果该年级有450名学生，那么据此估计大约有人最喜欢“乒乓球”．
（1）计算： 
；
（2）先化简，再求值：
其中x=4，y=－2．