如图，抛物线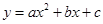
与
轴交于
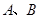两点，与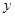
轴相交于点
．连结AC、BC，B、C两点的坐标分别为B（1，0）、
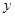，且当x=-10和x=8时函数的值相等．求a、b、c的值；
若点
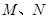同时从
点出发，均以每秒1个单位长度的速度分别沿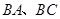
边运动，其中一个点到达终点时，另一点也随之停止运动．连结
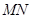，将
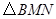沿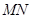翻折，当运动时间为几秒时，点恰好落在
边上的
处？并求点的坐标及四边形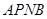
的面积；上下平移该抛物线得到新的抛物线，设新抛物线的顶点为D，对称轴与x轴的交点为E，若△ODE与△OBC相似，求新抛物线的解析式。
计算：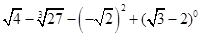 
.
求各式中的实数x.
（1）
；（2）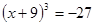
（本题10分）如图，矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上，且OD＝10，OB＝8．将矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合．
(1)直接写出点A、B的坐标：A(，)、B(，)；
(2)若抛物线y＝－
x2＋bx＋c经过点A、B，请求出这条抛物线的解析式；
(3)当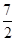
≤x≤7，在抛物线上存在点P，使△ABP的面积最大，那么△ABP最大面积是．（请直接写出结论，不需要写过程）
某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施，调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．
（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）
（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？
如图，过点B的直线l：
交y轴于点A，与反比例函数
的图象交于点C（2，n）和点D．
（1）求m和n的值，及另一交点D的坐标；
（2）求△COD的面积。