(本小题满分14分)
某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
| 分 组 |
[40 , 50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90 , 100] |
| 频 数 |
2 |
3 |
14 |
15 |
12 |
4 |
(1) 在这批树苗中任取一棵,其高度不低于80厘米的概率是多少?
(2)这批树苗的平均高度大约是多少?(计算时用各组的中间值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40 ,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?
△ABC的三个顶点A(-3,0),B(2,1),C(-2,3).求:
(Ⅰ)BC边上中线AD所在直线的方程;
(Ⅱ)BC边上高线AH所在直线的方程.
某几何体的三视图及其尺寸如下,求该几何体的表面积和体积.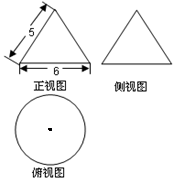
已知椭圆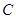 :
: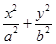 =1(a>b>0)与双曲线
=1(a>b>0)与双曲线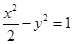 有公共焦点,且离心率为
有公共焦点,且离心率为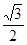 .
.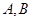 分别是椭圆
分别是椭圆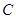 的左、右顶点.点
的左、右顶点.点 是椭圆
是椭圆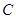 上位于
上位于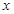 轴上方的动点.直线
轴上方的动点.直线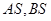 分别与直线
分别与直线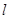 :
: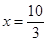 交于
交于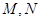 两点.
两点.
(I)求椭圆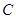 的方程;
的方程;
(II)当线段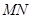 的长度最小时,在椭圆
的长度最小时,在椭圆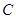 上是否存在点
上是否存在点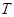 ,使得
,使得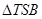 的面积为
的面积为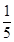 ?若存在,求出
?若存在,求出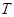 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.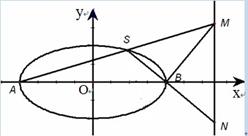
如右图,在平面直角坐标系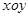 中,已知“葫芦”曲线
中,已知“葫芦”曲线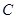 由圆弧
由圆弧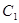 与圆弧
与圆弧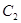 相接而成,两相接点
相接而成,两相接点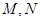 均在直线
均在直线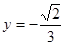 上.圆弧
上.圆弧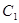 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点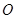 ,半径为
,半径为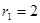 ;圆弧
;圆弧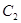 过点
过点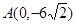 .
.
(I)求圆弧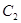 的方程;
的方程;
(II)已知直线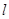 :
: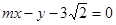 与“葫芦”曲线
与“葫芦”曲线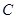 交于
交于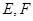 两点.当
两点.当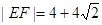 时,求直线
时,求直线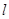 的方程.
的方程.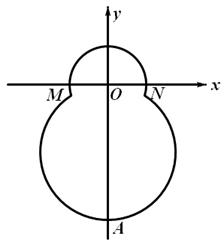
如图,在几何体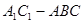 中,四边形
中,四边形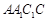 为平行四边形,且面
为平行四边形,且面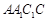
 面
面 ,
, ,且
,且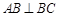 ,
,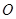 为
为 中点.
中点.
(Ⅰ)证明: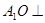 平面
平面 ;
;
(Ⅱ)求直线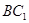 与平面
与平面 所成角的正弦值.
所成角的正弦值.