( 本题满分12分）(1)动手操作：
如图①，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点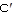
处，折痕为EF，若∠ABE=20°，那么
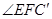的度数为 。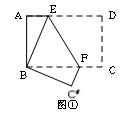
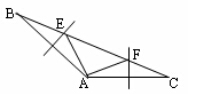
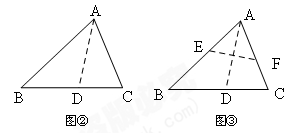
（2）观察发现小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由
（3）实践与运用：
将矩形纸片ABCD 按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP=MN=PQ（如图④）,求∠MNF的大小。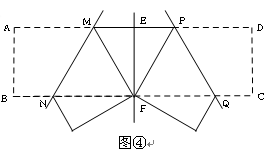
（1）如图1，
满足
．
①求
的值；
②若C（-6，0），连CB，作BE⊥CB，垂足为B，且BC=BE，连AE交
轴于P，求P点坐标．
（2）如图2，若A（6，0），B（0，3），点Q从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点Q运动时间为
秒，过Q点作直线AB的垂线，垂足为D，直线QD与轴交于E点，在点Q的运动过程中，一定存在△EOQ≌△AOB，请直接写出存在的值以及相应的E点坐标．
如图，将边长为8的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处，求：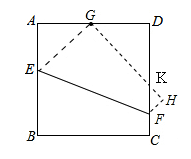
（1）线段BE的长；
（2）当∠DGK=450时，求四边形EFKG的面积．
如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．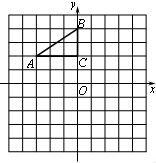
A1
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）移△ABC，若A的对应点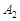
的坐标为（0，4），画出平移后对应的△
；
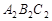（3）在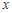
轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．
已知一次函数的图象过点（3，5）与（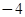
，
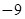），且该图象与x轴、y轴分别交于点A、点B，点O为坐标原点，
（1）求这个一次函数表达式；
（2）求△OAB的面积．
已知△ABC中∠BAC=150°，AB、AC的垂直平分线分别交BC于E、F．求∠EAF的度数．