在平面直角坐标系xOy中，已知抛物线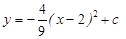
与x轴交于A、B两点（点A在点B的左侧），交y轴的正半轴于点C，其顶点为M，MH⊥x轴于点H，MA交y轴于点N，
＝
.
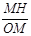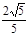（1）求此抛物线的函数表达式；
（2）过H的直线与y轴相交于点P，过O，M两点作直线PH的垂线，垂足分别为E，F，若 ＝时，求点P的坐标；
（3）将（1）中的抛物线沿y轴折叠，使点A落在点D处，连接MD，Q为（1）中的抛物线上的一点直线NQ交x轴于点G，当Q点在抛物线上运动时，是否存在点Q，使△ANG 与△ADM相似？若存在，求出所有符合条件的直线QG的解析式；若不存在，请说明理由．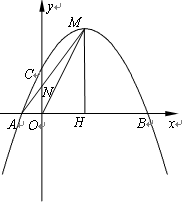
如图，AC是⊙O的直径，弦BD交AC于点E.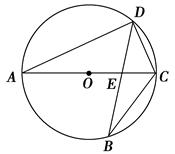
(1)求证：△ADE∽△BCE；
(2)如果AD2＝AE·AC，求证：CD＝CB.
如图，已知正方形ABCD中，BE平分∠DBC且交CD边于点E，将△BCE绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G.
(1)求证：△BDG∽△DEG；
(2)若EG·BG＝4，求BE的长．
如图，在正方形ABCD中，E是BC上的一点，连结AE，作BF⊥AE，垂足为H，交CD于F，作CG∥AE，交BF于G.
求证：(1)CG＝BH，
(2)FC2＝BF·GF，
(3)
＝
.
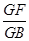如图，△ABC是一张锐角三角形的硬纸片，AD是边BC上的高，BC＝40 cm，AD＝30 cm，从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH，使它的一边EF在BC上，顶点G、H分别在AC、AB上，AD与HG的交点为M. 求矩形的长与宽．
如图，在Rt△ABC中，∠C＝90°，∠ABC的平分线交AC于点D，点O是AB上一点，⊙O过B、D两点，且分别交AB、BC于点E、F.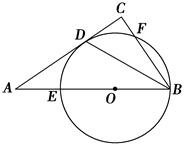
(1)求证：AC是⊙O的切线；
(2)已知AB＝10，BC＝6，求⊙O的半径r.