（本题10分）.今年春季，我国云南、贵州等西南地区遇到多少不遇旱灾，“一方有难，八方支援”，为及时灌溉农田，丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台（每种至少一台）及配套相同型号抽水机4台、3台、2台，每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时，灌溉农田32亩.(1)设甲种柴油发电机数量为x台，乙种柴油发电机数量为y台.①用含x、y的式子表示丙种柴油发电机的数量；②求出y与x的函数关系式；
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元，应如何安排三种柴油发电机的数量，既能按要求抽水灌溉，同时柴油发电机总费用W最少？
已知
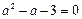，求代数式
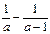的值．
如图, 已知：BF=DE,∠1=2，∠3=∠4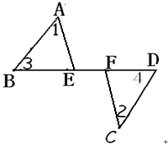
求证：AE=CF．
证明：
因式分解：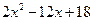
已知:在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD. 探究下列问题:
（1）如图1，当点D与点C位于直线AB的两侧时，a=b=3，且∠ACB=60°，则CD=；
（2）如图2，当点D与点C位于直线AB的同侧时，a=b=6，且∠ACB=90°，则CD=；
（3）如图3，当∠ACB变化,且点D与点C位于直线AB的两侧时，求 CD的最大值及相应的∠ACB的度数.
图1图2图3
已知：如图，在□ EFGH中，点F的坐标是（-2，-1），∠EFG=45°．
（1）求点H的坐标;
（2）抛物线
经过点E、G、H,现将向左平移使之
经过点F，得到抛物线
,求抛物线的解析式；
（3）若抛物线与y轴交于点A，点P在抛物线的对称轴上运动．请问：是否存在以AG为腰的等腰三角形AGP？若存在，求出点P的坐标；若不存在，请说明理由．