已知数列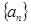 中,
中,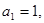 且点
且点 在直线
在直线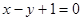 上。
上。
(Ⅰ)求数列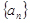 的通项公式;
的通项公式; (Ⅱ)若函数
(Ⅱ)若函数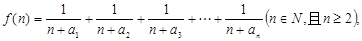 求函数
求函数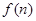 的最小值;
的最小值; (Ⅲ)设
(Ⅲ)设 表示数列
表示数列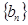 的前
的前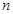 项和。试问:是否存在关于
项和。试问:是否存在关于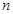 的整式
的整式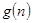 ,使得
,使得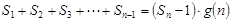 对于一切不小于2的自然数
对于一切不小于2的自然数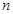 恒成立? 若存在,写出
恒成立? 若存在,写出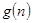 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
(本小题满分7分)选修4—2:矩阵与变换
已知矩阵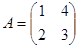
(Ⅰ)求A的逆矩阵A-1;
(Ⅱ)求A的特征值及对应的特征向量。
【改编】已知函数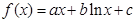 (
(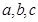 是常数)在
是常数)在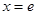 处的切线方程为
处的切线方程为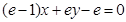 ,且
,且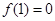 .
.
(Ⅰ)求常数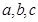 的值;
的值;
(Ⅱ)若函数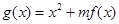 (
(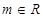 )在区间
)在区间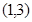 内不是单调函数,求实数
内不是单调函数,求实数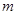 的取值范围;
的取值范围;
(Ⅲ)证明: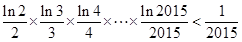 .
.
已知椭圆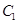 的方程为
的方程为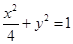 ,双曲线
,双曲线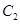 的左、右焦点分别为
的左、右焦点分别为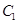 的左、右顶点,而
的左、右顶点,而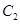 的左、右顶点分别是
的左、右顶点分别是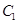 的左、右焦点。
的左、右焦点。
(1)求双曲线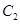 的方程;
的方程;
(2)若直线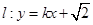 与椭圆
与椭圆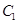 及双曲线
及双曲线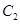 都恒有两个不同的交点,且L与的两个焦点A和B满足
都恒有两个不同的交点,且L与的两个焦点A和B满足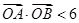 (其中O为原点),求
(其中O为原点),求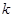 的取值范围。
的取值范围。
如图,三棱柱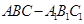 中,
中,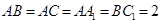 ,
,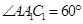 ,平面
,平面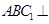 平面
平面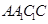 ,
,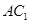 与
与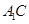 相交于点
相交于点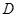 .
.
(Ⅰ)求证: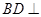 平面
平面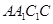 ;
;
(Ⅱ)求二面角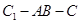 的余弦值.
的余弦值.
已知向量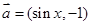 ,
,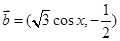 ,函数
,函数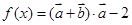 .
.
(1)求函数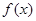 的最小正周期
的最小正周期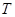 与值域;
与值域;
(2)已知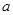 ,
,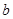 ,
,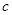 分别为
分别为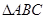 内角
内角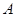 ,
, 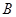 ,
,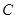 的对边,其中
的对边,其中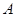 为锐角,
为锐角,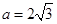 ,
, ,且
,且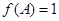 ,求
,求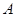 ,
,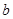 和
和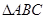 的面积
的面积 .
.