.(本小题满分12分)
若盒中装有同一型号的灯泡共 只,其中有
只,其中有 只合格品,
只合格品, 只次品.
只次品.
( 1 ) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求“
次,每次取一只灯泡,求“ 次中
次中 次取到次品”的概率;
次取到次品”的概率;
( 2 ) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求“成功更换会议室的已坏灯泡前取出的次品灯泡只数 ”的分布列和数学期望.
”的分布列和数学期望.
某化工厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。
在 中,
中,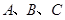 是三角形的三内角,
是三角形的三内角,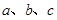 是三内角对应的三边,已知
是三内角对应的三边,已知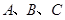 成等差数列,
成等差数列,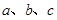 成等比数列
成等比数列
(Ⅰ)求角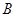 的大小;
的大小;
(Ⅱ)若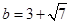 ,求
,求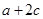 的值.
的值.
在数列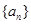 中,
中, ,当
,当 时,
时,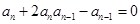
(Ⅰ)求数列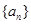 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知二次函数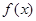 的二次项系数为
的二次项系数为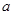 ,且不等式
,且不等式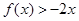 的解集为
的解集为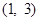 ,
,
(1)若方程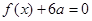 有两个相等的根,求
有两个相等的根,求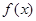 的解析式;
的解析式;
(2)若 的最大值为正数,求
的最大值为正数,求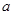 的取值范围.
的取值范围.
(1)若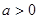 ,
,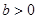 ,求证:
,求证: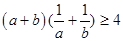 ;
;
(2)已知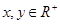 ,且
,且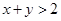 , 求证:
, 求证: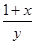 与
与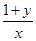 中至少有一个小于2.
中至少有一个小于2.