(14分)已知
、
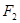是椭圆
的左、右焦点，A是椭圆上位于第一象限内的一点，点B也在椭圆上，且满足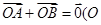
为坐标原点)，
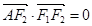，若椭圆的离心率等于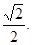
(1)求直线AB的方程； (2)若
的面积等于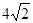
，求椭圆的方程；
(3)在(2)的条件下，椭圆上是否存在点M使得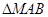
的面积等于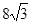
？若存在，求出点M的坐标；若不存在，说明理由.
（本小题满分12分）
如图，扇形AOB，圆心角AOB等于60°，半径为2，在弧AB上有一动点P，过P引平行于OB的直线和OA交于点C，设∠AOP＝θ，
求△POC面积的最大值及此时θ的值.
（本小题满分12分）
设
为数列
的前n项和，
，
，其中k是常数．
(1) 求
及
；
(2) 若对于任意的
，
，
，
成等比数列，求k的值．
（本小题满分10分） 已知
：方程
有两个不等的负实根，
：方程
无实根． 若或为真，且为假求实数
的取值范围。
（本小题满分12分）
已知函数
，a∈R
（1）若a =2，求函数
的单调区间；，
（2）若a =0，求证：
，
恒成立．
（本小题满分12分）
已知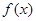
是R上的单调函数，且"x∈R，
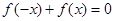，若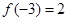
(1) 试判断函数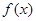在R上的增减性，并说明理由
(2) 解关于x的不等式
，其中m∈R且m > 0