平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足
=α
+β
,其中α,β∈R且α+β=1,则点C的轨迹方程为( )
| A．(x-1)2+(y-2)2=5 | B．3x+2y-11=0 |
| C．2x-y=0 | D．x+2y-5=0 |
已知非零向量e1,e2,a,b满足a=2e1-e2,b=ke1+e2.给出以下结论:
①若e1与e2不共线,a与b共线,则k=-2;
②若e1与e2不共线,a与b共线,则k=2;
③存在实数k,使得a与b不共线,e1与e2共线;
④不存在实数k,使得a与b不共线,e1与e2共线.
其中正确结论的个数是( )
| A．1个 | B．2个 | C．3个 | D．4个 |
已知A(2,-2),B(4,3),向量p的坐标为(2k-1,7)且p∥
,则k的值为( )
A．- |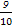
B． |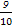
C．- |
D． |
已知向量a,b不共线,且
=a+4b,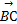
=-a+9b,
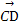=3a-b,则一定共线的是( )
| A．A,B,D | B．A,B,C |
| C．B,C,D | D．A,C,D |
若α,β是一组基底,向量γ=xα+yβ(x,y∈R),则称(x,y)为向量γ在基底α,β下的坐标,现已知向量a在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a在另一组基底m=(-1,1),n=(1,2)下的坐标为( )
| A．(2,0) | B．(0,-2) | C．(-2,0) | D．(0,2) |