如图,已知椭圆的中心在原点,焦点在 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 在
在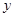 轴上的截距为
轴上的截距为 ,
, 交椭圆于A、B两个不同点.
交椭圆于A、B两个不同点.
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
下列命题正确的是()
①若数列 是等差数列,且
是等差数列,且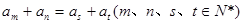 ,
,
则 ;
;
②若 是等差数列
是等差数列 的前
的前 项的和,则
项的和,则 成等差数列;
成等差数列;
③若 是等比数列
是等比数列 的前
的前 项的和,则
项的和,则 成等比数列;
成等比数列;
④若 是等比数列
是等比数列 的前
的前 项的和,且
项的和,且 ;(其中
;(其中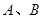 是非零常数,
是非零常数,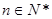 ),则
),则 为零.
为零.
| A.①② | B.②③ | C.②④ | D.③④ |
已知曲线 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,设点
,设点 (
( ).
).
(1)指出 ,并求
,并求 与
与 的关系式(
的关系式( );
);
(2)求 (
( )的通项公式,并指出点列
)的通项公式,并指出点列 ,
, ,
, ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由;
(3)令 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
设椭圆 的中心和抛物线
的中心和抛物线 的顶点均为原点
的顶点均为原点 ,
, 、
、 的焦点均在
的焦点均在 轴上,过
轴上,过 的焦点F作直线
的焦点F作直线 ,与
,与 交于A、B两点,在
交于A、B两点,在 、
、 上各取两个点,将其坐标记录于下表中:
上各取两个点,将其坐标记录于下表中:

(1)求 ,
, 的标准方程;
的标准方程;
(2)若 与
与 交于C、D两点,
交于C、D两点, 为
为 的左焦点,求
的左焦点,求 的最小值;
的最小值;
(3)点 是
是 上的两点,且
上的两点,且 ,求证:
,求证: 为定值;反之,当
为定值;反之,当 为此定值时,
为此定值时, 是否成立?请说明理由.
是否成立?请说明理由.
为了寻找马航 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在港口北偏东
方向航行,而在港口北偏东 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
, 海里,且
海里,且
 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口 正东
正东 海里的
海里的 处的补给船,速往小岛
处的补给船,速往小岛 装上补给物资供给科考船.该船沿
装上补给物资供给科考船.该船沿 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线 围成的三角形
围成的三角形 的面积
的面积 最小时,这种补给方案最优.
最小时,这种补给方案最优.
(1)求 关于
关于 的函数关系式
的函数关系式 ;
;
(2)应征调位于港口正东多少海里处的补给船只,补给方案最优?
如图,点A、B是单位圆 上的两点,点C是圆
上的两点,点C是圆 与
与 轴的正半轴的交点,将锐角
轴的正半轴的交点,将锐角 的终边
的终边 按逆时针方向旋转
按逆时针方向旋转 到
到 .
.
(1)若点A的坐标为 ,求
,求 的值;
的值;
(2)用 表示
表示 ,并求
,并求 的取值范围.
的取值范围.