如图，⊙O的直径AB＝10，CD是⊙O的弦，AC与BD相交于点P． 设∠BPC＝α，如果sinα是方程5x－13x＋6＝0的根，求cosα的值；
在(1)的条件下，求弦CD的长．
解方程组：
（1）
（2）
某市出租车车费标准如下：3km以内（含3km）收费8元；超过3km的部分每千米收费
1.6元.
（1）写出应收费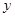
（元）出租车行驶路线
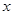（km）之间的关系式（其中
）
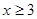（2）小亮乘出租车行驶4km，应付多少元？
（3）小波付车费16元，那么出租车行驶了多少千米？
如图，OP是∠AOC和∠BOD的平分线，OA = OC，OB = OD；
（1）图中∠1 =∠2吗？试说明理由.
（2）AB = CD吗？试说明理由.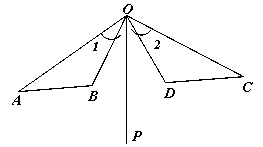
如图，一牧民从A点出发，到草地出发，到草地MN去喂马，该牧民在傍晚回到营帐B之前先带马去小河边PQ给马饮水（MN、PQ均为直线），试问牧民应走怎样的路线，才能使整个路程最短？（简要说明作图步骤，并在图上画出）