已知函数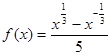 ,
, ;
;
(Ⅰ)证明 是奇函数;(Ⅱ)证明
是奇函数;(Ⅱ)证明 在(-∞,-1)上单调递增;
在(-∞,-1)上单调递增;
(Ⅲ)分别计算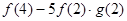 和
和 的值,由此概括出涉及函数
的值,由此概括出涉及函数 和
和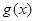 的对所有不等于零的实数
的对所有不等于零的实数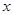 都成立的一个等式,并加以证明.
都成立的一个等式,并加以证明.
若函数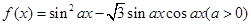 的图象与直线y=m相切,相邻切点之间的距离为
的图象与直线y=m相切,相邻切点之间的距离为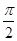 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且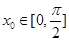 ,求点A的坐标.
,求点A的坐标.
已知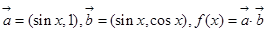
(1)若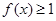 ,求x的范围;
,求x的范围;
(2)求 的最大值以及此时x的值.
的最大值以及此时x的值.
函数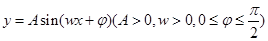 在
在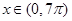 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当 时,
时,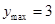 ;当
;当 时,
时,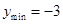 .(1)求此函数的解析式;(2)求此函数的单调递增区间.
.(1)求此函数的解析式;(2)求此函数的单调递增区间.
函数 的一段图象过点(0,1),如图所示.(1)求函数
的一段图象过点(0,1),如图所示.(1)求函数 的表达式;(2)将函数
的表达式;(2)将函数 的图象向右平移
的图象向右平移 个单位,得函数
个单位,得函数 的图象,求
的图象,求 的最大值,并求出此时自变量x的集合.
的最大值,并求出此时自变量x的集合.
如图所示,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3 cm,周期为3 s,且物体向右运动到A点(距平衡位置最远处)开始计时.(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式;(2)求该物体在t=5 s时的位置.