(本小题满分12分)
已知椭圆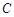 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线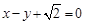 相切.
相切.
⑴求椭圆C的方程;
⑵设 ,
, 是椭圆
是椭圆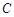 上的点,连结
上的点,连结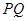 交椭圆
交椭圆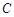 于另一点
于另一点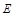 ,求直线
,求直线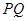 的斜率的取值范围.
的斜率的取值范围.
.已知函数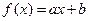 ,当
,当 时,值域为
时,值域为 ,当
,当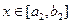 时,值域为
时,值域为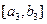 ,…,当
,…,当 时,值域为
时,值域为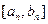 ,….其中a、b为常数,a1=0,b1=1.
,….其中a、b为常数,a1=0,b1=1.
(1)若a=1,求数列{an}与数列{bn}的通项公式;
(2)若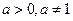 ,要使数列{bn}是公比不为1的等比数列,求b的值
,要使数列{bn}是公比不为1的等比数列,求b的值
已知抛物线 ,焦点为F,一直线
,焦点为F,一直线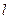 与抛物线交于A、B两点,且
与抛物线交于A、B两点,且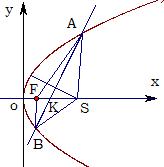
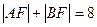 ,且AB的垂直平分线恒过定点S(6, 0)
,且AB的垂直平分线恒过定点S(6, 0)
①求抛物线方程;
②求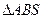 面积的最大值.
面积的最大值.
设一动直线过定点A(2, 0)且与抛物线 相交于B、C两点,点
相交于B、C两点,点
B、C在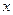 轴上的射影分别为
轴上的射影分别为 , P是线段BC上的点,且适合
, P是线段BC上的点,且适合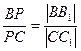 ,求
,求 的重心Q的轨迹方程,并说明该轨迹是什么图形.
的重心Q的轨迹方程,并说明该轨迹是什么图形.
抛物线 的焦点弦AB,求
的焦点弦AB,求 的值.
的值.
已知梯形ABCD中,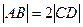 ,点E分有向线段
,点E分有向线段 所成的比为
所成的比为 ,双曲线过C、D、E三点,且以A、B为焦点,当
,双曲线过C、D、E三点,且以A、B为焦点,当 时,求双曲线离心率
时,求双曲线离心率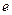 的取值范围.
的取值范围.