如图,在平面直角坐标系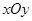 中,等边
中,等边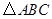 中,BC∥
中,BC∥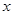 轴,且BC=
轴,且BC=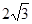 ,顶点A在抛物线
,顶点A在抛物线 上运动.
上运动.
(1)当顶点A运动至与原点重合时,顶点C是否在该抛物线上?
(2)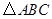 在运动过程中有可能被
在运动过程中有可能被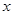 轴分成两部分,当上下两部分的面积之比为1:8(即
轴分成两部分,当上下两部分的面积之比为1:8(即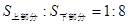 )时,求顶点A的坐标;
)时,求顶点A的坐标;
(3)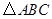 在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.
在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.
如图1,△ABC内接于半径为4cm的⊙O,AB为直径,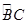 长为
长为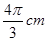 .
.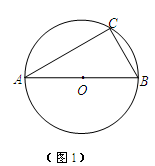
(1)计算∠ABC的度数;
(2)将与△ABC全等的△FED如图2摆放,使两个三角形的对应边DF与AC有一部分重叠,△FED的最长边EF恰好经过 的中点M.求证:AF=AB;
的中点M.求证:AF=AB;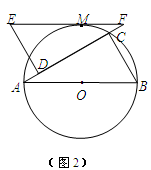
(3)设图2中以A、C、M为顶点的三角形面积为S,求出S的值.
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=DC,点E在对角线BD上,作∠ECF=90°,连接DF,且满足CF=EC.
(1)求证:BD⊥DF;
(2)当 时,试判断四边形DECF的形状,并说明理由.
时,试判断四边形DECF的形状,并说明理由.
已知:二次函数
 中的
中的 满足下表:
满足下表:
 |
 |
0 |
1 |
2 |
3 |
||
 |
0 |
 |
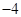 |
 |
 |
(1)求 的值;
的值;
(2)根据上表求 时的
时的 的取值范围;
的取值范围;
(3)若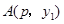 ,
, 两点都在该函数图象上,且
两点都在该函数图象上,且 ,试比较
,试比较 与
与 的大小.
的大小.
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且 .
.
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度(即AD+AB+BC).
(结果精确到0.1米.参考数据: ,
, ,
, )
)