将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去……
请你在右图中画出第一次分割的示意图;
若原正六边形的面积为
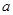 ,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
| 分割次数(n) |
1 |
2 |
3 |
…… |
| 正六边形的面积S |
|
|
|
|
观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数n有何关系?(S用含
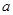 和n的代数式表示,不需要写出推理过程)
和n的代数式表示,不需要写出推理过程)
(.重庆市A卷,第26题,12分)如图1,在平面直角坐标系中,抛物线 交
交 轴于A,B两点(点A在点B的左侧),交
轴于A,B两点(点A在点B的左侧),交 轴于点W,顶点为C,抛物线的对称轴与
轴于点W,顶点为C,抛物线的对称轴与 轴的交点为D。
轴的交点为D。
图1
(1)求直线BC的解析式;
(2)点E(m,0),F(m+2,0)为 轴上两点,其中
轴上两点,其中 ,
, ,
, 分别垂直于
分别垂直于 轴,交抛物线与点
轴,交抛物线与点 ,
, ,交BC于点M,N,当
,交BC于点M,N,当 的值最大时,在
的值最大时,在 轴上找一点R,使
轴上找一点R,使 的值最大,请求出R点的坐标及
的值最大,请求出R点的坐标及 的最大值;
的最大值;
(3)如图2,已知 轴上一点
轴上一点 ,现以P为顶点,
,现以P为顶点, 为边长在
为边长在 轴上方作等边三角形QPG,使GP⊥
轴上方作等边三角形QPG,使GP⊥ 轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为
轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为 ,设
,设 与△ADC的重叠部分面积为s,当点
与△ADC的重叠部分面积为s,当点 到
到 轴的距离与点
轴的距离与点 到直线AW的距离相等时,求s的值。
到直线AW的距离相等时,求s的值。
|

(.河南省,第23题,11分)如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F. 点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.
(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值. 进而猜想:对于任意一点P,PD与PF的差为定值. 请你判断该猜想是否正确,并说明理由;
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.
请直接写出所有“好点”的个数,并求出△PDE的周长最小时“好点”的坐标.
(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)
已知:如图, 是半圆
是半圆 的直径,弦
的直径,弦 ,动点
,动点 、
、 分别在线段
分别在线段 、
、 上,且
上,且 ,
, 的延长线与射线
的延长线与射线 相交于点
相交于点 、与弦
、与弦 相交于点
相交于点 (点
(点 与点
与点 、
、 不重合),
不重合), ,
, .设
.设 ,
, 的面积为
的面积为 .
.

(1)求证: ;
;
(2)求 关于
关于 的函数关系式,并写出它的定义域;
的函数关系式,并写出它的定义域;
(3)当 是直角三角形时,求线段
是直角三角形时,求线段 的长.
的长.
(本题满分12分,每小题满分各4分)
已知在平面直角坐标系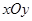 中(如图),抛物线
中(如图),抛物线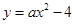 与
与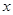 轴的负半轴相交于点
轴的负半轴相交于点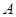 ,与
,与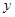 轴相交于点
轴相交于点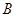 ,
,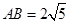 .点
.点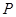 在抛物线上,线段
在抛物线上,线段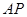 与
与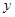 轴的正半轴交于点
轴的正半轴交于点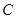 ,线段
,线段 与
与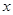 轴相交于点
轴相交于点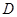 .设点
.设点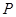 的横坐标为
的横坐标为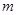 .
.
(1)求这条抛物线的解析式;
(2)用含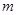 的代数式表示线段
的代数式表示线段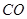 的长;
的长;
(3)当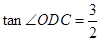 时,求
时,求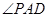 的正弦值.
的正弦值.
胡老师计划组织朋友暑假去革命圣地延安两日游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费。假设组团参加甲、乙两家旅行社两日游的人数均为x人。
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数
关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你通过计算,在甲、乙两家旅行社中,
帮助胡老师选择收取总费用较少的一家。