如图所示,质量为M、长度为L的木板静止在光滑的水平面上,质量为m的小物体(可视为质点)放在木板上最左端,现用一水平恒力F作用在小物体上,使物体从静止开始做匀加速直线运动.已知物体和木板之间的摩擦力为Ff.当物体滑到木板的最右端时,木板运动的距离为x,则在此过程中( )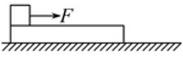
| A.物体到达木板最右端时具有的动能为(F-Ff)(L+x) |
| B.物体到达木板最右端时,木板具有的动能为Fx |
| C.物体克服摩擦力所做的功为FfL |
| D.物体和木板增加的机械能为Fx |
现有一段长L=0.2 m、通有电流I=2.5 A的直导线,则关于此导线在磁感应强度为B的磁场中所受磁场力F的情况,下列说法正确的是( )
| A.如果B=2 T,则F一定为1 N |
| B.如果F=0,则B也一定为零 |
| C.如果B=4 T,则F有可能为1 N |
| D.当F为最大值时,通电导线一定与B平行 |
磁性水雷是用一个可绕轴转动的小磁针来控制起爆电路的,军舰被地磁场磁化后就变成了一个浮动的磁体.当军舰接近磁性水雷时,就会引起水雷的爆炸,其依据是( )
| A.磁体的吸铁性 |
| B.磁极间的相互作用规律 |
| C.电荷间的相互作用规律 |
| D.磁场对电流的作用原理 |
如图所示,A、B两均匀直杆上端分别用细线悬挂于天花板上,下端搁在水平地面上,处于静止状态,悬挂A杆的绳倾斜,悬挂B杆的绳恰好竖直,则关于两杆的受力情况,下列说法中正确的有( )
(A).A、B都受三个力作用
(B).A、B都受四个力作用
(C).A受三个力,B受四个力
(D).A受四个力,B受三个力
合力与分力下列说法中正确的是()
| A.合力的大小一定大于每一个分力的大小 |
| B.合力的大小至少大于其中一个分力的大小 |
| C.合力的大小可能比每一个分力都大也有可能比每一个分力都小 |
| D.合力的大小可能与两个分力的大小相等 |
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧。在这过程中下面木块移动的距离为()
A. |
B. |
C. |
D. |