已知函数 在区间[0,1]上的最大值为3,求实数a的值。
在区间[0,1]上的最大值为3,求实数a的值。
对划艇运动员甲、乙二人在相同条件下进行6次测试,测得他们的速度的数据
如下:甲:27,38,30,37,35,31
乙:33,29,38,34,28,36
根据以上数据判断,谁更优秀。
用辗转相除法求5280与12155的最大公约数。
如图,在长方体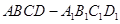 中,
中,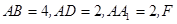 是棱
是棱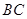 的中点,点
的中点,点 在棱
在棱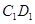 上,且
上,且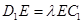 (
(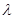 为实数).
为实数).
(1)当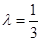 时,求直线
时,求直线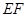 与平面
与平面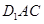 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)试问:直线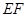 与直线
与直线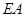 能否垂直?请说明理由.
能否垂直?请说明理由.
抛掷A,B,C三枚质地不均匀的纪念币,它们正面向上的概率如下表所示 ;
;
| 纪念币 |
A |
B |
C |
| 概率 |
 |
a |
a |
将这三枚纪念币同时抛掷一次,设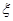 表示出现正面向上的纪念币的个数.
表示出现正面向上的纪念币的个数.
(1)求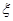 的分布列及数学期望;
的分布列及数学期望;
(2)在概率 中,若
中,若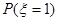 的值最大,求a的最大值
的值最大,求a的最大值