如图,在长方体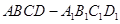 中,
中,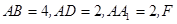 是棱
是棱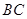 的中点,点
的中点,点 在棱
在棱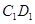 上,且
上,且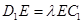 (
(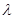 为实数).
为实数).
(1)当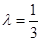 时,求直线
时,求直线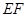 与平面
与平面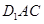 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)试问:直线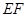 与直线
与直线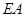 能否垂直?请说明理由.
能否垂直?请说明理由.
设集合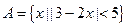 ,
,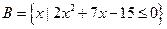 ,
,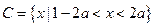 .
.
(1)若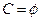 ,求实数
,求实数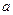 的取值范围.
的取值范围.
(2)若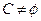 且
且 ,求实数
,求实数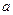 的取值范围.
的取值范围.
已知m>1,直线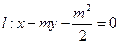 ,椭圆
,椭圆 ,
,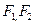 分别为椭圆
分别为椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线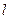 过右焦点
过右焦点 时,求直线
时,求直线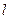
 的方程;
的方程;
(Ⅱ)设直线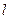 与椭圆
与椭圆 交于
交于 两点,
两点,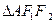 ,
,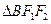 的重心分别为
的重心分别为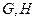 .若原点
.若原点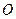 在以线段
在以线段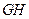 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围.
的取值范围. 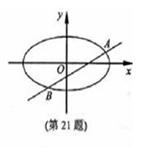
已知椭圆 ,试确定m的取值范围,使得椭圆上总有不同的两点关于直线y=4x+m对称。
,试确定m的取值范围,使得椭圆上总有不同的两点关于直线y=4x+m对称。
(本小题满分12分)已知椭圆C: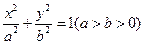 的离心率
的离心率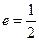 ,且原点
,且原点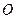 到直线
到直线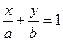 的距离为
的距离为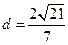 .
.
(Ⅰ)求椭圆的方程 ;
(Ⅱ)过点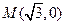 作直线与椭圆C交于
作直线与椭圆C交于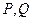 两点,求
两点,求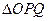 面积的最大值.
面积的最大值.
四.附加题 (共20分,每小题10分)
已知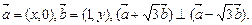
(1)点P(x,y)的轨迹C的方程;
(2)若直线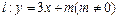 与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.
与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.