设集合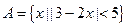 ,
,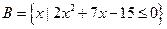 ,
,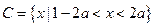 .
.
(1)若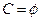 ,求实数
,求实数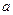 的取值范围.
的取值范围.
(2)若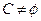 且
且 ,求实数
,求实数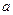 的取值范围.
的取值范围.
椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且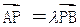 .
.
(1)求椭圆方程;
(2)若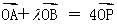 ,求m的取值范围.
,求m的取值范围.
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当 f(x)取得最大值时,求二面角D-BF-C的余弦值.

一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: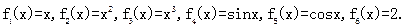
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.
若函数 的定义域为
的定义域为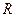 ,求实数
,求实数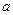 的取值范围.
的取值范围.
已知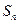 为数列
为数列 的前
的前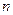 项和,且
项和,且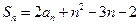 ,
,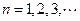 ,(Ⅰ)求证:数列
,(Ⅰ)求证:数列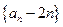 为等比数列;(Ⅱ)设
为等比数列;(Ⅱ)设 ,求数列
,求数列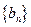 的前
的前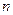 项和
项和 ;(Ⅲ)设
;(Ⅲ)设 ,数列
,数列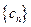 的前
的前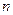 项和为
项和为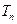 ,求证:
,求证: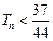 .
.