已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当 f(x)取得最大值时,求二面角D-BF-C的余弦值.

检测部门决定对某市学校教室的 空气质量进行检测,空气质量分为A、B、C三级.
空气质量进行检测,空气质量分为A、B、C三级.
每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格.设各教室的空气质量相互独立,且每次检测的结果也相互独立.根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为 ,
, ,
, .
.
(1) 在该市的教室中任取一间,估计该间教室空气质量合格的概率;
(2) 如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为X,并以空气质量为A级的频率作为空气质量为A级的概率,求X的分布列及期望值.
(本小题满分12分)
已知函数 论函数
论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现在采用分层抽样法(层内采用不放回的简单随机抽样)从甲,乙两组中共抽取3人进行技术考核.
(1)求甲,乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工的概率;
(3)令X表示抽取的3名工人中男工人的人数,求X的分布列及数学期望.
已知函数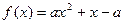 (
(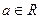 )
)
(1)若函数 有最大值
有最大值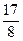 ,求实数a的值; (2)解不等式
,求实数a的值; (2)解不等式 (a∈R).
(a∈R).
(本小题满分12分)
已知命题 ,命题
,命题
 ,
,
若命题 是真命题,求实数a的取值范围.
是真命题,求实数a的取值范围.