椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且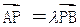 .
.
(1)求椭圆方程;
(2)若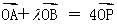 ,求m的取值范围.
,求m的取值范围.
已知斜三棱柱 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成角为
,侧棱与底面所成角为 ,点
,点 在底面上射影D落在BC上.
在底面上射影D落在BC上.
(Ⅰ)求证: 平面
平面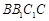 ;
;
(Ⅱ)若点D恰为BC中点,且 ,求
,求 的大小;
的大小;
(III)若 ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小.
已知数列{an}的前n项和为Sn,点(n,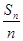 )在直线y=
)在直线y= x+
x+ 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=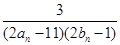 ,数列{cn}的前n项和为Tn,求使不等式Tn>
,数列{cn}的前n项和为Tn,求使不等式Tn> 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用 力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为
力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为 (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(Ⅰ)求某个家庭得分为 的概率?
的概率?
(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.请问某个家庭获奖的概率为多少?
(Ⅲ)若共有5个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.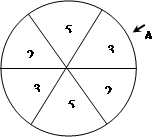
(本小题满分10分)设函数
(1)求函数 取最值时x的取值集合;
取最值时x的取值集合;
(2)在△ABC中,角A、B、C的对边分别是a,b,c,且满足 求函数
求函数 的取值范围.
的取值范围.
设 是给定的正整数,有序数组
是给定的正整数,有序数组 同时满足下列条件:
同时满足下列条件:
①  ,
,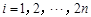 ; ②对任意的
; ②对任意的 ,都有
,都有 .
.
(1)记 为满足“对任意的
为满足“对任意的 ,都有
,都有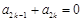 ”的有序数组
”的有序数组 的个数,求
的个数,求 ;
;
(2)记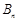 为满足“存在
为满足“存在 ,使得
,使得 ”的有序数组
”的有序数组 的个数,求
的个数,求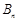 .
.