(本小题12分)如图,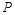 、
、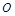 分别是正四棱柱
分别是正四棱柱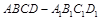 上、下底面的中
上、下底面的中
心,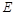 是
是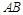 的中点,
的中点,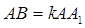 .
.
(Ⅰ)求证: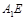 ∥平面
∥平面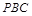 ;
;
(Ⅱ当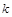 取何值时,
取何值时,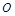 在平面
在平面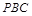 内的射影恰好为
内的射影恰好为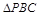 的重心?
的重心?

本小题满分12分)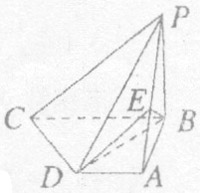
如图,在四棱锥P-ABCD中,PB⊥底面 ,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。(1)求异面直线PA与CD所成的角;(2)求证:PC∥平面EBD;(3)求二面角A-BE-D的大小。
,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。(1)求异面直线PA与CD所成的角;(2)求证:PC∥平面EBD;(3)求二面角A-BE-D的大小。
(理)已知椭圆 的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.(1)求椭圆C1的方程;(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;(3)设C2与x轴交于点Q,不同的两点R、S在C2上,且满足
,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.(1)求椭圆C1的方程;(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;(3)设C2与x轴交于点Q,不同的两点R、S在C2上,且满足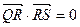 ,求
,求 的取值范围.
的取值范围.
(理)某校有一贫困学生因病需手术治疗,但现在还差手术费1.1万元.团委计划在全校开展爱心募捐活动,为了增加活动的趣味性吸引更多学生参与,特举办“摇奖100%中奖”活动.凡捐款10元便可享受一次摇奖机会,如图是摇奖机的示意图,摇奖机的旋转盘是均匀的,扇形区域A,B,C,D,E所对应的圆心角的比值分别为1:2:3:4:5.相应区域分别设立一、二、三、四、五等奖,奖品分别为价值5元、4元、3元、2元、1元的学习用品.摇奖时,转动圆盘片刻,待停止后,固定指针指向哪个区域(边线忽略不计)即可获得相应价值的学习用品(如图指针指向区域,可获得价值3元的学习用品).(1)预计全校捐款10元者将会达到1500人次,那么除去购买学习用品的款项后,剩余款项是否能帮助该生完成手术治疗?(2)如果学生甲捐款20元,获得了两次摇奖机会,求他获得价值6元时的学习用品的概率.
设函数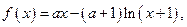 其中
其中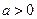 。(1)求
。(1)求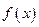 的单调区间;
的单调区间;
(2)当 时,证明不等式:
时,证明不等式: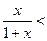


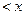 ;
;
(3)设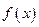 的最小值为
的最小值为 证明不等式:
证明不等式: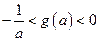 。
。
(文)已知函数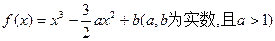 在区间
在区间 上最大值为1,最小值为
上最大值为1,最小值为 2.(1)求
2.(1)求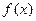 的解析式;(2)若函数
的解析式;(2)若函数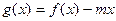 在区间
在区间 上为减函数,求实数m的取值范围.
上为减函数,求实数m的取值范围.