(本题满分10分)
如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA＝AB＝BC＝2，E为PA的中点，过E作平行于底面的平面EFGH，分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形，AD∥BC，AB⊥AD，∠BCD=135°.
(1)求异面直线AF与BG所成的角的大小；
(2)求平面APB与平面CPD所成的锐二面角的余弦值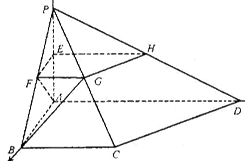
围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用的旧墙需维修），其他三面围墙要新建，在旧墙对面的新墙上要留一个宽度为2m的进出口，如图所示已知旧墙的维修
费用为45元/m，新墙的造价为180元/m，设利用的旧墙长
度为x（单位：m），修建此矩形场地围墙的总费用为y（单位：元）
⑴将y表示为x的函数；
⑵写出f(x)的单调区间（不必证明）
⑶根据⑵，试确定x，
使修建此矩形场地围墙的总费用最小，并求出最小总费用。
已知函数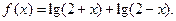
（1）
求函数
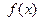的定义域；
（2）记函数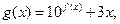
求
函数
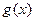的值域；
（3）若不等式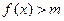
有解，求实数
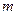的取值范围.
本题满分14分）已知z是复数，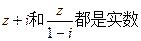
，⑴求复数z；⑵设关于
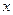的方程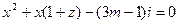
有实根，求纯虚数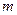
已知函数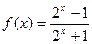
，（1）判断
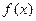的奇偶性；（2）判断并用定义证明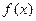在
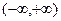上的单调性
若集合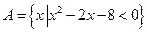
，
．
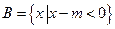（1）若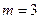
，全集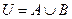
,试求全集U及
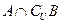；（2）若
,求实数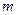
的取值范围；