已知函数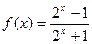 ,(1)判断
,(1)判断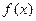 的奇偶性;(2)判断并用定义证明
的奇偶性;(2)判断并用定义证明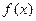 在
在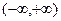 上的单调性
上的单调性
(本小题满分1 2分)在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
(I)求点P的轨迹C的方程;
(Ⅱ)若Q是轨迹C上异于点P的一个点,且 ,直线OP与QA交于点M,试探究:点M的横
,直线OP与QA交于点M,试探究:点M的横 坐标是否为定值?并说明理由.
坐标是否为定值?并说明理由.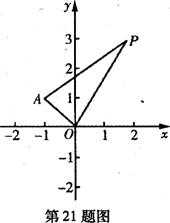
(本小题满分l 2分)某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15一O.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价 格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
(I)每套丛 书定价为100元时,书商能获得的总利润是多少万元?
书定价为100元时,书商能获得的总利润是多少万元?
(Ⅱ)每套丛书定价为多少元时,单套丛书的利润最大?
.(本小题满分1 2分)设△ABC的内角A 、B、C所对的边分别为a、b、c.已知a=3,B=
、B、C所对的边分别为a、b、c.已知a=3,B= ,S△ABC=6
,S△ABC=6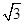
( I )求△ABC的周长;
(Ⅱ)求sin2A的值 .
.
(本小题满分12分)已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子 里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(I)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性
最大?请说明理由. ’
.(本小题满分l 2分) 已知{an}是等比数列,a1=2,且a1,a3+1,a4成等差数列.
(I)求数列{a n}的通项公式;
(Ⅱ)若bn=log2 an,求数列{bn}的前n项和Sn.