(本小题满分5分)已知二次函数y= x2 +4x+3.(1)用配方法将y= x2 +4x+3化成y=a (x-h) 2 +k的形式,写出函数的最值;
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)写出当x为何值时,y>0.
化简: .
计算: .
如图,抛物线 与 轴交于 , 两点.
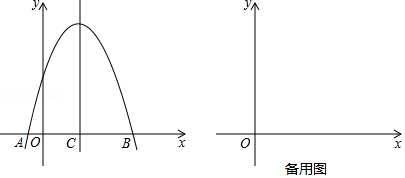
(1)若过点 的直线 是抛物线的对称轴.
①求抛物线的解析式;
②对称轴上是否存在一点 ,使点 关于直线 的对称点 恰好落在对称轴上.若存在,请求出点 的坐标;若不存在,请说明理由.
(2)当 , 时,函数值 的最大值满足 ,求 的取值范围.
阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.
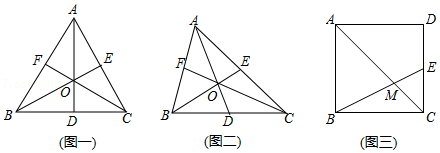
(1)特例感知:如图(一 ,已知边长为2的等边 的重心为点 ,求 与 的面积.
(2)性质探究:如图(二 ,已知 的重心为点 ,请判断 、 是否都为定值?如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图(三 ,在正方形 中,点 是 的中点,连接 交对角线 于点 .
①若正方形 的边长为4,求 的长度;
②若 ,求正方形 的面积.
习近平总书记说:"读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气".某校为提高学生的阅读品味,现决定购买获得第十届茅盾文学奖的《北上》(徐则臣著)和《牵风记》(徐怀中著)两种书共50本.已知购买2本《北上》和1本《牵风记》需100元;购买6本《北上》与购买7本《牵风记》的价格相同.
(1)求这两种书的单价;
(2)若购买《北上》的数量不少于所购买《牵风记》数量的一半,且购买两种书的总价不超过1600元.请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?