(本小题满分12分)2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
| 动作 |
K |
D |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
 |
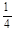 |
 |
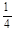 |
乙系列:
| 动作 |
K |
D |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
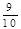 |
 |
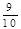 |
 |
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I) 若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II) (II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
已知函数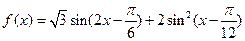 。
。
①求函数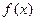 的最小正周期和单调递增区间
的最小正周期和单调递增区间 ;
;
②若 ,求函数
,求函数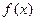 的最大值及取最大值时对应的
的最大值及取最大值时对应的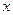 值。
值。
(本小题满分12分)
已知抛物线 (
( )的焦点为椭圆
)的焦点为椭圆 的右焦点,点
的右焦点,点 、
、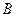 为抛物线上的两点,
为抛物线上的两点,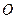 是抛物线的顶点,
是抛物线的顶点,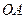 ⊥
⊥ .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求证:直线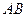 过定点
过定点 ;
;
(Ⅲ)设弦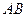 的中点为
的中点为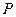 ,求点
,求点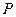 到直线
到直线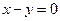 的距离的最小值.
的距离的最小值.
(本小题满分12分) 已知函数
已知函数 ,设
,设 ,
,
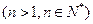 .
. (Ⅰ)求
(Ⅰ)求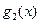 ,
, 的表达式,并直接写出
的表达式,并直接写出 的表达式;
的表达式;
(Ⅱ)设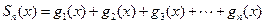 ,
,
若关于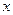 的函数
的函数
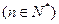 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
(本 小题满分12分)
小题满分12分)
已知函数 (
(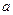 为常数).(Ⅰ)若
为常数).(Ⅰ)若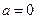 ,解不等式
,解不等式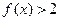 ;
;
(Ⅱ)解关于 的不等式
的不等式 .
.
(本小题满分13分)
已知函数 .
.
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)设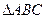 的内角
的内角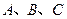 的对边分别为
的对边分别为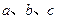 ,且
,且 ,若向量
,若向量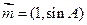 与
与 向量
向量 共线
共线 ,求
,求 的值.
的值.