如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0). 试写出点A,B之间的距离d(厘米)与时间t(秒)之间的函数表达式;
问点A出发后多少秒两圆相切?

如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)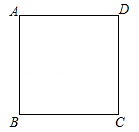
如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
(1)求证:四边形EGFH是矩形;
(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.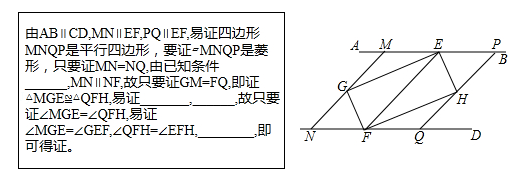
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1,60)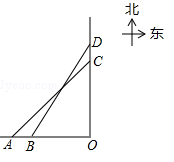
某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.
(1)求取出纸币的总额是30元的概率;
(2)求取出纸币的总额可购买一件51元的商品的概率.
为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图: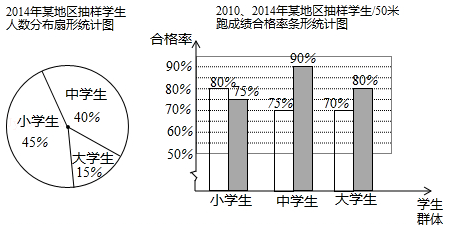
(1)本次检测抽取了大、中、小学生共名,其中小学生名;
(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为名;
(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.