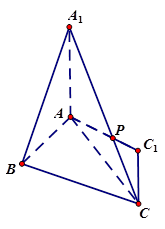
.如图,直三棱柱ABC-A1B1C1中,AB⊥AC, D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC;
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小.
求经过直线 与圆
与圆 的交点,且经过点
的交点,且经过点 的圆的
的圆的
方程.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,
SA⊥底面ABCD,M为SA的中点,N为CD的中点.
⑴证明:平面SBD⊥平面SAC;
⑵证明:直线MN//平面SBC.
已知两直线 :
: ,
,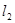 :
: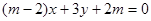 ,当
,当 为何值时,直线
为何值时,直线 与
与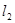 :⑴平行; ⑵垂直.
:⑴平行; ⑵垂直.
设椭圆 的左、右焦点分别为
的左、右焦点分别为
 ,
, 是椭圆上位于
是椭圆上位于 轴上方的动点 (Ⅰ)当
轴上方的动点 (Ⅰ)当 取最小值时,求
取最小值时,求 点的坐标;
点的坐标;
(Ⅱ)在(Ⅰ)的情形下,是否存在以 为直角顶点的内接于椭圆的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
为直角顶点的内接于椭圆的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
.如图, 中,
中,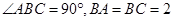 ,分别过
,分别过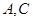 作平面
作平面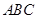 的垂线
的垂线 和
和 ,连结
,连结 和
和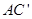 交于点
交于点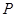 .
.
(Ⅰ)设点 为
为 中点,若
中点,若 ,求证:直线
,求证:直线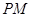 与平面
与平面 平行;
平行;
(Ⅱ)设 为
为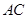
 中点,二面角
中点,二面角 等于
等于 ,求直线
,求直线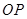 与平面
与平面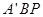 所成角
所成角
的大小.