已知直线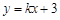 (
(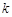 <0)分别交
<0)分别交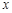 轴、
轴、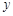 轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作
轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作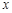 轴的垂线交直线AB于点C,设运动时间为
轴的垂线交直线AB于点C,设运动时间为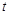 秒.
秒.
(1)当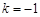 时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出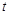 =1秒时C、Q两点的坐标;
=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求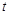 的值.
的值.
(2)当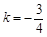 时,设以C为顶点的抛物线
时,设以C为顶点的抛物线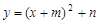 与直线AB的另一交点为D
与直线AB的另一交点为D
(如图2),①求CD的长;
②设△COD的OC边上的高为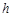 ,当
,当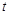 为何值时,
为何值时,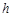 的值最大?
的值最大?
代入求值: ,其中
,其中 .
.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.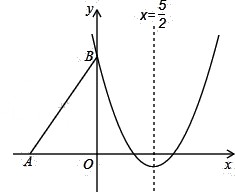
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中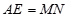 .准备在形如Rt
.准备在形如Rt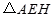 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形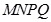 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
| 品种 |
红色花草 |
黄色花草 |
紫色花草 |
| 价格(元/米2) |
60 |
80 |
120 |
设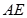 的长为
的长为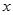 米,正方形
米,正方形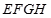 的面积为
的面积为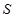 平方米,买花草所需的费用为
平方米,买花草所需的费用为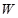 元,解答下列问题:
元,解答下列问题:
(1)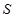 与
与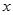 之间的函数关系式为
之间的函数关系式为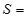 ;
;
(2)求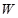 与
与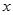 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.
已知:关于x的一元二次方程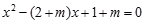
(1)求证:方程有两个实数根;
(2)设m<0,且方程的两个实数根分别为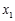 ,
,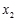 (其中
(其中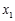 <
<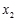 ),若y是关于m的函数,且
),若y是关于m的函数,且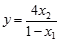 ,求这个函数的解析式;
,求这个函数的解析式;
(3)在(2)的条件下,利用函数图象求关于m的方程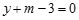 的解。
的解。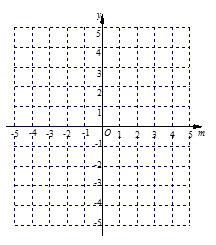
如图,在平面直角坐标系中,反比例函数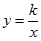 (
(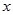 >0)的图象和矩形ABCD的第一象限,AD平行于
>0)的图象和矩形ABCD的第一象限,AD平行于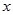 轴,且AB=2,AD=4,点A的坐标为(2,6).
轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.