（本小题满分10分）
观察控究，完成证明和填空．
如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H，得到的四边形EFGH叫中点四边形．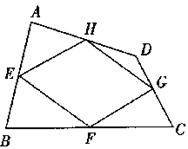
（1）求证：四边形EFGH是平行四边形
；（2）如图，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：
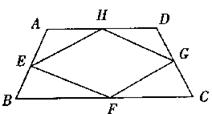
当四边形ABCD变成平行四边形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成矩形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成菱形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；
当四边形ABCD变成正方形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；（3）根据
以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的？
如图，抛物线y = ax2 + bx + 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长及H点的坐标；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．
已知，如图，在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC，笔山职中数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°，然后他们沿着坡度为1：2．4的斜坡AP攀行了26米，在坡顶A处又测得该塔的塔顶B的仰角为76°．求：
（1）坡顶A到地面PO的距离；（2）移动信号发射塔BC的高度（结果精确到1米）．
（参考数据：sin76°≈0．97，cos76°≈0．24，tan76°≈4．01）
如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=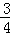
．
（1）求⊙O的半径长；
（2）求线段CF长．
已知关于x的方程
，
（1）求证：方程恒有两个不相等的实数根．
（2）此方程的一根为1，请求出方程的另一根，并求出以此两根为边的直角三角形的三角形的周长．
（ 10分）课外阅读是提高学生素养的重要途径，笔山职中为了了解学校学生的阅读情况，组织调查组对全校三个年级共1500名学生进行了抽样调查，抽取的样本容量为300，已知该校有初一学生600名，初二学生500名，初三学生400名．
（1）为使调查的结果更加准确地反映全校的总体情况，应分别在初一年级随机抽取人；在初二年级随机抽取人；在初三年级随机抽取人（请直接填空）．
（2）调查组对本校学生课外阅读量的统计结果分别用扇形统计图和频数分布直方图表示如下，请根据上统计图，计算样本中各类阅读量的人数，并补全频数分布直方图．
（3）根据（2）的调查结果，从该校中随机抽取一名学生，他最大可能的阅读量是多少本？为什么？