如图，抛物线y = ax2 + bx + 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长及H点的坐标；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．
在△ABC中，∠A＝90°，点D在线段BC上，∠EDB＝
∠C，BE⊥DE，垂足为E，DE与AB相交于点F．
（1）当AB＝AC时，（如图1），
①∠EBF＝°
②探究线段BE与FD的数量关系，并加以证明；
（2）当AB＝kAC时（如图2），求
的值（用含k的式子表示）．
某商家计划从厂家采购空调和冰箱两种产品共20台，空调的采购单价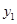
（元/台）与采购数量
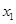（台）满足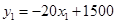
（
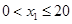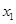，为整数）；冰箱的采购单价
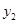（元/台）与采购数量
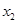（台）满足
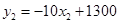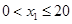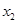（，为整数）．
（1）经商家与厂家协商，采购空调的数量不少于冰箱数量的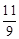
，且空调采购单价不低于1200元，问该商家共有几种进货方案？
（2）该商家分别以1760元／台和1700元／台的销售单价售出空调和冰箱，且全部售完．在（1）的条件下，问采购空调多少台时总利润最大？并求最大利润．
已知关于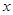
的一元二次方程
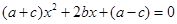，其中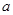
、
、
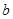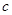分别为△ABC三边的长．
（1）如果
是方程的根，试判断△ABC的形状，并说明理由：
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点．
（1）求证：AC2＝AB·AD；
（2）求证：CE∥AD；
（3）若AD＝4， AB＝6，求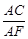
的值．
如图，已知二次函数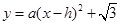
的图象经过原点0（0，0），A（2，0）．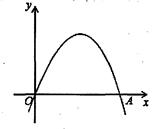
（1）写出该函数图象的对称轴；
（2）若将线段OA绕点O逆时针旋转60°到OA'，试判断点A'是否在该函数图象上？