已知关于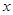 的一元二次方程
的一元二次方程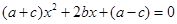 ,其中
,其中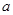 、
、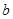 、
、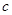 分别为△ABC三边的长.
分别为△ABC三边的长.
(1)如果 是方程的根,试判断△ABC的形状,并说明理由:
是方程的根,试判断△ABC的形状,并说明理由:
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
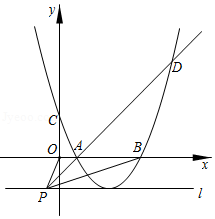
如图所示,二次函数 的图象(记为抛物线 与 轴交于点 ,与 轴分别交于点 、 ,点 、 的横坐标分别记为 , ,且 .
(1)若 , ,且过点 ,求该二次函数的表达式;
(2)若关于 的一元二次方程 的判别式△ .求证:当 时,二次函数 的图象与 轴没有交点.
(3)若 ,点 的坐标为 , ,过点 作直线 垂直于 轴,且抛物线的 的顶点在直线 上,连接 、 、 , 的延长线与抛物线 交于点 ,若 ,求 的最小值.
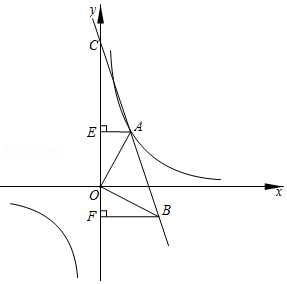
如图所示, 的顶点 在反比例函数 的图象上,直线 交 轴于点 ,且点 的纵坐标为5,过点 、 分别作 轴的垂线 、 ,垂足分别为点 、 ,且 .
(1)若点 为线段 的中点,求 的值;
(2)若 为等腰直角三角形, ,其面积小于3.
①求证: ;
②把 称为 , , , 两点间的“ 距离”,记为 ,求 , , 的值.
是 的直径,点 是 上一点,连接 、 ,直线 过点 ,满足 .
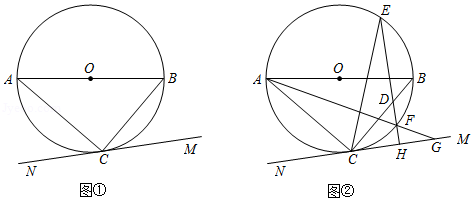
(1)如图①,求证:直线 是 的切线;
(2)如图②,点 在线段 上,过点 作 于点 ,直线 交 于点 、 ,连接 并延长交直线 于点 ,连接 ,且 ,若 的半径为1, ,求 的值.
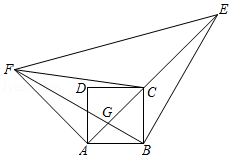
如图所示, 的顶点 在正方形 对角线 的延长线上, 与 交于点 ,连接 、 ,满足 .
(1)求证: .
(2)若正方形 的边长为1, ,求 的值.
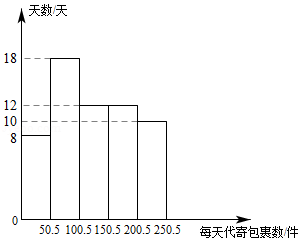
近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
(1)求该数据中每天代寄包裹数在 范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包裹中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
|
重量 (单位:千克) |
|
|
|
|
件数(单位:件) |
15 |
10 |
15 |
求这40件包裹收取费用的平均数.