如图,两矩形ABCD,ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.
(1) 求证:MN丄平面ABCD
(2) 求线段AB的长;
(3) 求二面角A—DE—B的平面角的正弦值.
(本小题满分10分)选修4-5:不等式选讲
对于任意的实数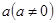 和
和 ,不等式
,不等式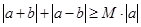 恒成立,记实数
恒成立,记实数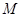 的最大值是
的最大值是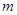 .
.
(1)求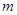 的值;(2)解不等式
的值;(2)解不等式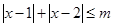 .
.
(本小题满分10分)【选修4—1:几何证明选讲】
在直角坐标系中,以原点为极点,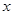 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线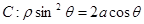
 ,已知过点
,已知过点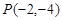 的直线
的直线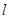 的参数方程为
的参数方程为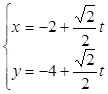 (
(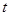 为参数),直线
为参数),直线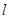 与曲线
与曲线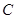 分别交于
分别交于 两点。
两点。
(1)写出曲线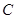 和直线
和直线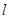 的普通方程;
的普通方程;
(2)若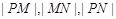 成等比数列,求
成等比数列,求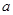 的值.
的值.
(本小题满分10分)【选修4—1:几何证明选讲】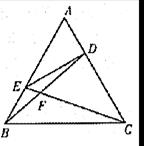
如图,在正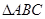 中,点
中,点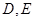 分别在边
分别在边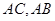 上,且
上,且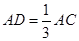 ,
,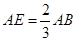 ,
,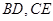 相交于点
相交于点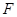
(1)求证: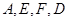 四点共圆;
四点共圆;
(2)若正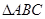 的边长为2,求,
的边长为2,求,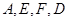 所在圆的半径.
所在圆的半径.
(本小题满分12分)已知函数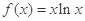 (
(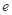 为无理数,
为无理数,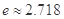 )
)
(1)求函数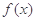 在点
在点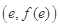 处的切线方程;
处的切线方程;
(2)设实数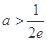 ,求函数
,求函数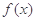 在
在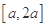 上的最小值;
上的最小值;
(3)若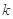 为正整数,且
为正整数,且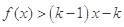 对任意
对任意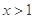 恒成立,求
恒成立,求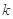 的最大值.
的最大值.
(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2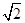 ,C1H⊥平面AA1B1B,且C1H=
,C1H⊥平面AA1B1B,且C1H=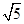 .
.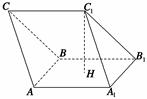
(1)求异面直线AC与A1B1所成角的余弦值;
(2)求二面角A-A1C1-B1的正弦值;
(3)设N为棱B1C1的中点,点M在平面AA1B1B内,且MN⊥平面A1B1C1,求线段BM的长.