如图(1)在正方形ABCD中,对角线AC与BD相交于点E,AF平分于∠BAC,交BD于点F。

求证:EF+- AC =AB
点C1从C出发,沿着线段CB向点B运动(不与点B重合),同时点A1从A出发,沿着BA的延长线运动,点C1与点A1的运动速度相同,当运点C1停止运动时,另一动点A1也随之停止运动。如图(2)A1、F1平分∠BA∠BA1C1,交BD于F1,过点F1作F1E1⊥A1C1,垂足为E1,请猜想E1 F1,
 A1C1,与AB三者之间的数量关系,并证明你的猜想
A1C1,与AB三者之间的数量关系,并证明你的猜想在(2)的条件下,当A1E1=3,C1E1=2,求BD的长。
在下图的圆圈里有5个实数,请计算其中有理数的和与无理数的积的差。
阅读下列材料,并解决后面的问题。
材料:一般的,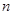 个相同的因数
个相同的因数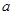 相乘:
相乘: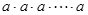 记为
记为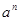 ,如
,如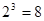 ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为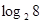 (即
(即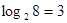 )。一般的,若
)。一般的,若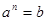 (
(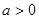 且
且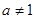 ,
,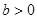 ),则
),则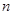 叫做以
叫做以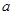 为底
为底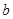 的对数,记为
的对数,记为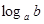 (即
(即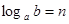 ),如
),如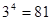 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为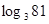 (即
(即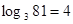 )。
)。
问题:(1)计算以下各对数的值: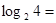 ,
,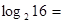 ,
,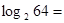 ;
;
(2)观察(1)中三数4、16、64之间满足怎样的关系式?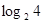 、
、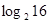 、
、 之间又满足怎样的关系式?
之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗?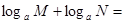 (
(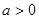 且
且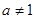 ,
,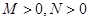 );
);
已知,BC//OA,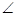 B=
B=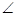 A=100°,试回答下列问题:
A=100°,试回答下列问题:
(1)如下图所示,求证:OB//AC。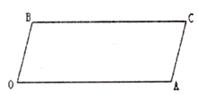
(2)如下图,若点E、F在BC上,且满足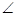 FOC=
FOC=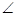 AOC,并且OE平分
AOC,并且OE平分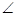 BOF。
BOF。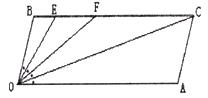
(i)求: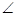 EOC的度数;
EOC的度数;
(ii)求: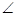 OCB:
OCB: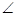 OFB的值。
OFB的值。
(iii)如下图,若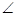 OEB=
OEB=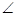 OCA,此时
OCA,此时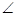 OCA度数等于。(在横线上填上答案即可)。
OCA度数等于。(在横线上填上答案即可)。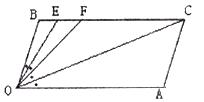
某高科技公司根据市场需求,计划生产A、B两种型号的医疗器械,其部分信息如下,信息一:A、B两种型号的医疗器械共生产80台。
信息二:该公司所筹生产医疗器械资金不少于1800万元,但不超过1810万元。且把所筹资金全部用于生产此两种医疗器械。
信息三:A、B两种医疗器械的生产成本和售价如下表:
| 型号 |
A |
B |
| 成本(万元/台) |
20 |
25 |
| 售价(万元/台) |
24 |
30 |
根据上述信息。解答下列问题:
请问:该公司对此两种医疗器械有哪几种生产方案?哪种生产方案能获得最大利润
为了配合学校开展的“爱护地球母亲”主题活动,初一年级提出“我骑车我快乐”的口号。四月1日之后小明不用父母开车送,坚持自己骑车上学,四月底他对自己家的用车情况进行了统计,四月份所走的总路程比三月份的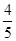 还少100千米,且这两个月共消耗93号汽油260升。若小明家的汽车平均油耗为0.1升/千米,求他家三、四两月各行驶了多少千米。
还少100千米,且这两个月共消耗93号汽油260升。若小明家的汽车平均油耗为0.1升/千米,求他家三、四两月各行驶了多少千米。