我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例。如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了
（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律。例如，在三角形中第三行的三个数1，2，1，恰好对应
展开式中的系数;第四行的四个数1，3，3，1，恰好对应着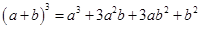
展开式中的系数等等。
（1）根据上面的规律，写出
的展开式。
（2）利用上面的规律计算：
已知xm=2,xn=3,求x2m+n的值.
计算：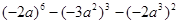
计算：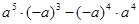
如图，△ABC中，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图象经过点B、D．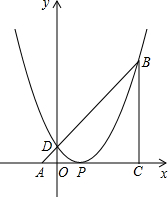
（1）用m的代数式表示点A、D的坐标；
（2）求这个二次函数关系式；
（3）点Q（x，y）为二次函数图象上点P至点B之间的一点，连接PQ、BQ，当x为何值时，四边形ABQP的面积最大？
某商店经销一种成本为每千克40元的产品，若按每千克50元销售，一个月能售出500千克. 销售单价每涨1元，月销售量就减少10千克，针对这种产品，请解答以下问题：
（1）当销售单价定为每千克55元时，计算销售量与月销售利润；
（2）商店想在销售额不超过20000元的情况下，使得月销售利润达到8000元，则销售单价应为多少？