设椭圆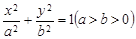 的左,右两个焦点分别为
的左,右两个焦点分别为 ,短轴的上端点为
,短轴的上端点为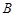 ,短轴上的两个三等分点为
,短轴上的两个三等分点为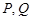 ,且
,且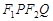 为正方形。
为正方形。
(1)求椭圆的离心率;
(2)若过点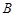 作此正方形的外接圆的切线在
作此正方形的外接圆的切线在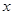 轴上的一个截距为
轴上的一个截距为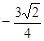 ,求此椭圆方程。
,求此椭圆方程。
已知各项均为正数的数列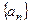 前
前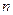 项和为
项和为 ,首项为
,首项为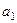 ,且
,且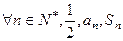 成等差数列.
成等差数列.
(1)求数列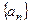 的通项公式;
的通项公式;
(2)若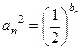 ,设
,设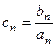 ,求数列
,求数列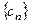 的前
的前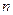 项和
项和 .
.
已知函数
 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(1)求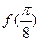 的值;
的值;
(2)将函数y=f(x)的图象向右平移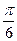 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
已知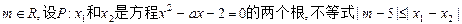 对任意实数
对任意实数 恒成立;Q:函数
恒成立;Q:函数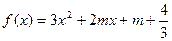 有两个不同的零点. 求使“P∧Q”为真命题的实数m的取值范围.
有两个不同的零点. 求使“P∧Q”为真命题的实数m的取值范围.
在△ABC中,角A,B,C所对的边分别为a,b,c.已知 ,且满足
,且满足 .
.
(1)求角A的大小;
(2)若||+||=||,试判断△ABC的形状.
14分)已知椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1),且其右焦点到直线x-y+ =0的距离为3.(I)求椭圆的方程;
=0的距离为3.(I)求椭圆的方程;
(II)是否存在斜率为k(k≠0)的直线l,使l与已知椭圆交于不同的两点M、N,
且|AN|=|AM|?若存在,求出k的取值范围;若不存在,请说明理由.