如图,在四棱锥A-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.
(1)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(2)求证:平面BDE⊥平面SAC;
(3)当二面角E-BD-C的大小为45°时,试判断点E在SC上的位置,并说明理由.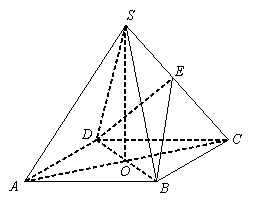
若a,b是两个不共线的非零向量,t∈R.若|a|=|b|=2且a与b夹角为60°,t为何值时,|a-tb|的值最小?
已知定义在R上的奇函数 f(x)有最小正周期2,且当x∈(0,1)时, f(x)= .
.
(1)求 f(x)在[-1,1]上的解析式;
(2)证明: f(x)在(0,1)上是减函数.
已知sinα= ,求tan(α+
,求tan(α+ )+
)+ .
.
已知函数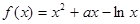 ,
, 
(Ⅰ)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅱ)令 ,是否存在实数
,是否存在实数 ,当
,当
 (
( 是自然常数)时,函数
是自然常数)时,函数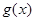 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(III)当
 时,证明:
时,证明: 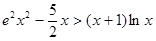
已知斜三棱柱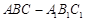 的底面是直角三角形,
的底面是直角三角形,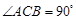 ,侧棱与底面所成角为
,侧棱与底面所成角为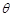 ,点
,点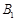 在底面上射影D落在BC上.
在底面上射影D落在BC上.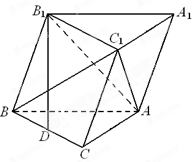
(Ⅰ)求证: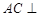 平面
平面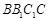 ;
;
(Ⅱ)若点D恰为BC中点,且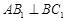 ,求
,求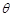 的大小;
的大小;
(III)若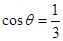 ,且当
,且当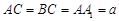 时,求二面角
时,求二面角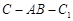 的大小.
的大小.