(本小题满分16分)
设数列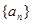 的前项和为
的前项和为 ,已知
,已知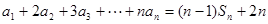 (
( ).
).
(1)求 的值;
的值;
(2)求证:数列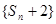 是等比数列;
是等比数列;
(3)抽去数列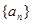 中的第1项,第4项,第7项,……,第
中的第1项,第4项,第7项,……,第 项,……,余下的项顺序不变,组成一个新数列
项,……,余下的项顺序不变,组成一个新数列 ,若
,若 的前
的前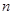 项的和为
项的和为 ,求证:
,求证: .
.
市中心医院用甲、乙两种药片为手术后的病人配制营养餐,已知甲种药片每片含5单位的蛋白质和10单位的铁质,售价为3元;乙种药片每片含7单位的蛋白质和4 单位的铁质,售价为2元。若病人每餐至少需要35单位的蛋白质和40单位的铁质,应使用甲、乙两种药片各几片才能既满足营养要求又使费用最省?
解关于 的不等式:
的不等式: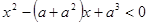
设 ,求函数
,求函数 的最小值及相应
的最小值及相应 的值.
的值.
已知椭圆 的离心率为
的离心率为 ,定点M(1,0),椭圆短轴的端点是B1,B2,且
,定点M(1,0),椭圆短轴的端点是B1,B2,且
(1)求椭圆C的方程;
(2)设过点M且斜率不为0的直线交椭圆C于A,B两点.试问x轴上是否存在定点P,使PM平分∠APB?若存在,求出点P的坐标;若不存在,说明理由,
已知函数 .
.
(1)若函数f(x)的图象在 处的切线斜率为3,求实数m的值;
处的切线斜率为3,求实数m的值;
(2)求函数f(x)的单调区间;
(3)若函数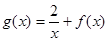 在[1,2]上是减函数,求实数m的取值范围.
在[1,2]上是减函数,求实数m的取值范围.