解关于 的不等式:
的不等式: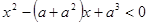
已知函数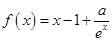 (
(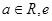 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于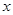 轴,求
轴,求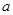 的值;
的值;
(2)讨论函数 的极值情况;
的极值情况;
(3)当 时,若直线
时,若直线 与曲线
与曲线 没有公共点,求k的取值范围.
没有公共点,求k的取值范围.
已知椭圆E的长轴的一个端点是抛物线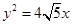 的焦点,离心率是
的焦点,离心率是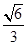 .
.
(1)求椭圆E的标准方程;
(2)已知动直线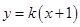 与椭圆E相交于A、B两点,且在
与椭圆E相交于A、B两点,且在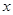 轴上存在点M,使得
轴上存在点M,使得 与k的取值无关,试求点M的坐标.
与k的取值无关,试求点M的坐标.
已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是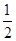 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记“ ”为事件A,求事件A的概率;
”为事件A,求事件A的概率;
②在区间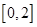 内任取2个实数
内任取2个实数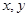 ,求事件“
,求事件“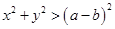 恒成立”的概率.
恒成立”的概率.
如图,在四棱锥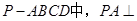 平面ABCD,
平面ABCD, ,E为PD的中点,F在AD上且
,E为PD的中点,F在AD上且 .
.
(1)求证:CE//平面PAB;
(2)若PA=2AB=2,求四面体PACE的体积.
已知数列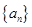 中,
中,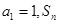 为其前
为其前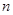 项和,且对任意
项和,且对任意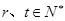 ,都有
,都有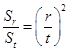 .
.
(1)求数列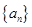 的通项公式;
的通项公式;
(2)设数列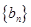 满足
满足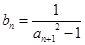 ,求数列
,求数列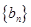 的前
的前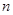 项和
项和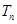 .
.