已知椭圆 的离心率为
的离心率为 ,定点M(1,0),椭圆短轴的端点是B1,B2,且
,定点M(1,0),椭圆短轴的端点是B1,B2,且
(1)求椭圆C的方程;
(2)设过点M且斜率不为0的直线交椭圆C于A,B两点.试问x轴上是否存在定点P,使PM平分∠APB?若存在,求出点P的坐标;若不存在,说明理由,
(本小题满分14分)已知函数 .
.
(Ⅰ)当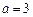 时,求
时,求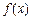 的单调递增区间;
的单调递增区间;
(Ⅱ)求证:曲线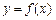 总有斜率为
总有斜率为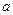 的切线;
的切线;
(Ⅲ)若存在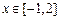 ,使
,使 成立,求
成立,求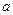 的取值范围.
的取值范围.
如图,已知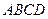 为平行四边形,
为平行四边形,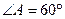 ,
,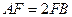 ,
,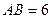 ,点
,点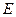 在
在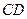 上,
上, ,
, ,
,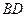 交
交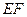 于点
于点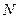 ,现将四边形
,现将四边形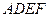 沿
沿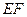 折起,使点
折起,使点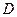 在平面
在平面 上的射影恰在直线
上的射影恰在直线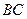 上.
上.
(Ⅰ) 求证: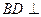 平面
平面 ;
;
(Ⅱ) 求折后直线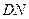 与直线
与直线 所成角的余弦值;
所成角的余弦值;
(Ⅲ) 求三棱锥 的体积.
的体积.
(本小题满分12分)
已知向量
(1)求a·b及|a+b|;
(2)若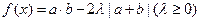 的最小值是
的最小值是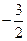 ,求实数
,求实数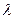 的值。
的值。
(本小题满分12分)已知函数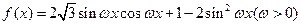 ,
,
且函数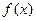 的最小正周期为
的最小正周期为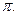
(1)若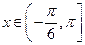 ,求函数
,求函数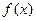 的单调递减区间;
的单调递减区间;
(2)将函数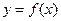 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的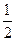 ,把所得到的图象再向左平移
,把所得到的图象再向左平移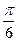 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间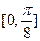 上的最小值。
上的最小值。
(本小题满分12分)如图,在底面是菱形的四棱锥P—ABCD中,∠ABC= ,PA=AC=a,PB=PD=
,PA=AC=a,PB=PD=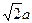 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.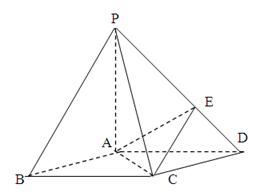
(I)证明PA⊥平面ABCD;
(II)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论