在边长为2的正方体 中,E是BC的中点, F是
中,E是BC的中点, F是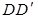 的中点
的中点
(1) 求证:CF∥平面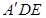
求二面角 的平面角的余弦值。
的平面角的余弦值。
已知函数 .
.
(1)当 时,求f (
时,求f (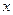 )的值域;
)的值域;
(2)将f (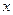 )的图象按向量
)的图象按向量 ="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量
="(h," k) (0 < h < p)平移,使得平移后的图象关于原点对称,求出向量 .
.
(本题10分)已知函数 有极值.
有极值.
(1)求 的取值范围;
的取值范围;
(2)若 在
在 处取得极值,且当
处取得极值,且当 时,
时, 恒成立,求
恒成立,求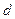 的取值范围.
的取值范围.
(本题10分)已知椭圆与双曲线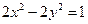 共焦点,且过(
共焦点,且过(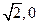 )
)
(1)求椭圆的标准方程;
(2)求斜率为2的一组平行弦的中点轨迹方程。
(本题8分)在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
(本题8分)已知p: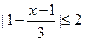 ,q:
,q: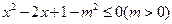 ,若
,若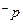 是
是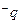 的必要不充分条件,求实数m的取值范围。
的必要不充分条件,求实数m的取值范围。